Definitions
Random or Stochastic Process
A stochastic process is generally viewed as a family of random variables,
or a collection of a large number of records that describe a physical
phenomenon. The records can be a function of time {xk(t)}
or frequency {xk(f)}. Each record
is somewhat different from any other record. It is impossible therefore
to include all possible records in the analysis. Instead, a random process
is described in terms of statistical properties. Each load in a random
vibration study is a random process. The response of a model to these
loads is also a random process described in statistical terms.
Autocorrelation Function
The autocorrelation function of a random process describes the correlation
between the values in a record at different instants of time. It is defined
as the expected value of the product of a random variable x(t)
with a time-shifted version of itself.
 (Eq.1)
(Eq.1)
Root Mean Square (rms)
The mean square value provides a measure of the energy associated with
the random process.
It is defined as the value of the autocorrelation function for t
= 0
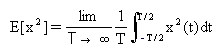 (Eq.2),
(Eq.2),
where
E is called
the expectation operator. The positive square root of the mean value is
known as the root
mean square, or rms.
Variance
The mean square value of a random process about its mean mx.
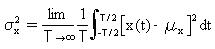 (Eq.3)
(Eq.3)
The positive square root of the variance is known as standard
deviation.
Power Spectral Density (psd)
The power spectral density is defined as the Fourier
transform of the autocorrelation function of a random process.
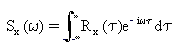 (Eq.4)
(Eq.4)
Power spectral density describes how the energy of the random process
is distributed in the frequency domain.
White Noise
A white noise signal has a uniform power spectral density in all frequencies.
In other words, the signal's energy is distributed equally in all frequencies.
Related Topics
Random
Vibration Analysis