When to Use Dynamic Analysis
Static studies assume that loads are constant or applied very slowly
until they reach their full values. Because of this assumption, the velocity
and acceleration of each particle of the model is assumed to be zero.
As a result, static studies neglect inertial and damping forces.
For many practical cases, loads are not applied slowly or they change
with time or frequency. For such cases, use a dynamic study. Generally
if the frequency of a load is larger than 1/3 of the lowest (fundamental)
frequency, a dynamic study should be used.
Linear dynamic studies are based on frequency studies. The software
calculates the response of the model by accumulating the contribution
of each mode to the loading environment. In most cases, only the lower
modes contribute significantly to the response. The contribution of a
mode depends on the load’s frequency content, magnitude, direction, duration,
and location.
Objectives of a dynamic analysis include:
Design structural
and mechanical systems to perform without failure in dynamic environments.
Modify system's characteristics
(i.e., geometry, damping mechanisms, material properties, etc.) to reduce
vibration effects.
Equations of Motion
Single Degree of Freedom (SDOF) Systems
Consider the simple mass-spring system. The
mass (m) is subjected to a force F(t) in the u direction as, a function
of time. The mass is allowed to move in the u direction only and hence
this is a Single-Degree-Of-Freedom (SDOF) system. The motion is resisted
by a spring of stiffness (k)
.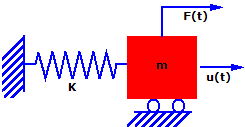
Writing Newton's Second Law (force equals
mass times acceleration) for this system at time (t) results in:
F(t)-ku(t) = mu..(t)
or:
mu..(t)
+ ku(t) = F(t)
where:
u..(t)
is the acceleration of the mass at time (t) and it is equal to the second
derivative of u with respect to time
k = is the stiffness of the spring
Theoretically, if the mass is displaced and
released, it will continue to vibrate with the same amplitude forever.
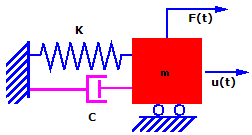
In practice, the mass vibrates with progressively smaller amplitudes until
it comes to rest. This phenomenon is called damping and it is caused by
loss of energy through friction and other effects. Damping is a complex
phenomenon. For the purpose of this discussion, assume that the damping
force is proportional to the velocity. This type of damping is called
viscous damping.
Considering damping, the above equation becomes:
mu..(t)
+ cu.(t) + ku(t) = F(t)
where:
u.(t)
is the velocity of the mass at time (t), and it is equal to the first
derivative of u with respect to time
Note:
In static studies, velocity and acceleration are so small that they can
be neglected and F and u are not functions of time. The above equation
reduces to: F=ku.
Multi Degree of Freedom (MDOF) Systems
For a Multi-Degree-of-Freedom (MDOF) system,
m, c, and k become matrices instead of single values and the equations
of motion are expressed as:
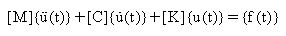 , where
, where
[M]:
mass matrix
[K]
: stiffness matrix
[C]
: damping matrix
{u(t)}:
displacement vector at time t (displacement components of every node)
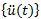 acceleration
vector at time t (acceleration components of every node)
acceleration
vector at time t (acceleration components of every node)
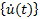 velocity vector at time t
(velocity components of every node)
velocity vector at time t
(velocity components of every node)
{f(t)}:
time varying load vector (force components of every node)
Related Topics
Linear
Static Versus Linear Dynamic Analysis
Dynamic
Loads
Loads
and Result Options for Dynamic Analysis