Kriechmodelle
Kriechen ist eine zeitabhängige Dehnung, die unter Dauerspannung entsteht.
Sie tritt in den meisten Maschinenbaumaterialien auf – insbesondere
bei Metallen, die hohen Temperaturen ausgesetzt werden, Kunststoffen mit
hohem Polymergehalt, Beton sowie Festtreibstoffen in Raketentriebwerken.
Da Kriecheffekte sich über einen längeren Zeitraum entwickeln, werden
sie in der dynamischen Analyse im Allgemeinen vernachlässigt.
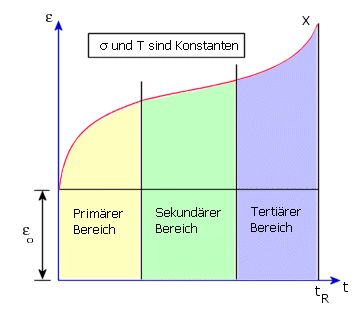
Die Kriechkurve ist die grafische Darstellung der Dehnung in Abhängigkeit
von der Zeit. Drei verschiedene Bereiche lassen sich in einer Kriechkurve
unterscheiden: primärer, sekundärer und tertiärer Bereich (siehe nachfolgende
Abbildung). In der Regel sind die primären und sekundären Bereiche von
Interesse.
Zwei Kriechgesetze auf Grundlage einer Zustandsgleichung wurden implementiert.
Jedes Gesetz definiert eine Gleichung für die uniaxiale Kriechdehnung
hinsichtlich der uniaxialen Spannung und Zeit.
Klassisches Kriechgesetz (Bailey-Norton-Gesetz)
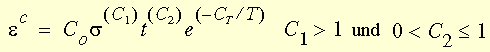
Zeichenerklärung:
T
= Temperatur (Kelvin) (= Eingangstemperatur + Referenztemperatur + Temperaturunterschied)
CT = Eine Materialkonstante, die die
Kriechtemperatur-Abhängigkeit definiert
Das klassische Kriechgesetz stellt primäre und sekundäre Bereiche in
einer Formel dar. Tertiäre Kriechbereiche werden nicht berücksichtigt.
„t“
steht für die aktuelle, reale Zeit (nicht die Pseudo-Zeit) und s
für die uniaxiale Gesamtspannung zur Zeit t.
Zur Erweiterung dieser Gesetze auf das Kriechverhalten bei mehreren
Achsen gelten folgende Annahmen:
Das uniaxiale Kriechgesetz bleibt weiterhin gültig,
wenn die uniaxiale Kriechdehnung und die uniaxiale Spannung durch ihre
effektiven Werte ersetzt werden.
Das Material ist isotrop.
Die Kriechdehnungen sind nicht komprimierbar.
Bei einer numerischen Kriechanalyse, bei der unter Umständen eine zyklische
Belastung erfolgt, werden die aktuellen Kriechdehnungsraten auf Grundlage
der Dehnungshärtungsregel als Funktion der aktuellen Spannung und der
Gesamtkriechdehnung ausgedrückt:
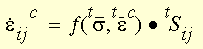
Zeichenerklärung:
