Nitinol-Materialmodell

Formgedächtnislegierungen wie Nitinol zeigen einen superelastischen Effekt. Mit dem Begriff „Superelastisch“ werden Materialien beschrieben, die großen Verformungen in Belastungs-/Entlastungszyklen ausgesetzt werden können, ohne permanente Verformungen aufzuweisen. In der Tat zeigt das Material unter Belastungs-/Entlastungszyklen, sogar bei Dehnungen bis zu 10 - 15 %, eine hysteretische Reaktion, einen Steif-weich-steif-Pfad für Belastung und Entlastung und keine permanente Verformung.

Das Nitinol-Materialmodell ist für Volumenkörper- und Schalenelemente verfügbar.

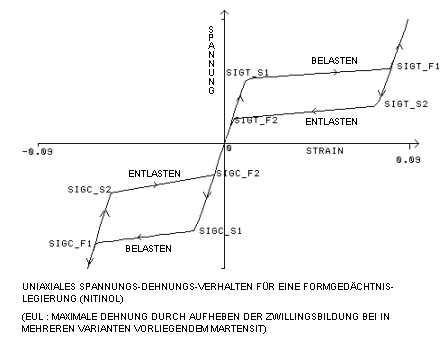
Eine typische Spannungs-/Dehnungsreaktion für einen Nitinol-Stab unter uniaxialen Lastbedingungen. Beachten Sie, dass sich das Material bei Zugspannung und Kompression unterschiedlich verhält.

Die Spannungs-/Dehnungskurve von Formgedächtnislegierungen zeigt ein erkennbares makroskopisches Verhalten, das in traditionellen Materialien nicht zu finden ist. Dieses Verhalten ist der zugrunde liegenden Makromechanik zuzuschreiben.

In Formgedächtnislegierungen finden reversible martensitische Phasentransformationen statt, d. h. diffusionslose Festkörper-Festkörper-Transformationen zwischen einer kristallografisch geordneteren Phase, „Austenit“, und einer kristallografisch weniger geordneten Phase, „Martensit“.

Die weichen Teile der Reaktionskurve stellen die Bereiche dar, bei denen eine Phasentransformation, eine Umwandlung von Austenit in Martensit (Belastung) und von Martensit in Austenit (Entlastung), stattfindet.

Zur Vereinfachung werden wir das weiche Verhalten auf der Reaktionskurve als „plastisch“ und die steifen Bereiche als „elastisch“ bezeichnen.

Nach dieser Definition verhält sich das Material zuerst elastisch, bis eine bestimmte Spannung erreicht ist (die anfängliche Fließspannung beim Belasten). Wenn die Belastung zunimmt, zeigt das Material ein elastoplastisches Verhalten, bis die plastische Dehnung den entsprechenden Höchstwert erreicht. Von diesem Punkt an verhält sich das Material unter wachsenden Lasten wieder elastisch.

Beim Entlasten beginnt das Material immer elastisch, bis die Spannung auf die ursprüngliche Fließspannung beim Entlasten verringert wird. Das Material wird dann auf elastoplastische Weise entlastet, bis die gesamte akkumulierte plastische Dehnung (von der Belastungsphase) verloren ist. Von dieser Stelle an wird das Material elastisch entlastet, bis es in seine ursprüngliche Form (keine permanente Verformung) bei Spannung 0 unter Last 0 zurückkehrt.

Die Nitinol-Modellformel

Da Nitinol gewöhnlich wegen seiner Fähigkeit verwendet wird, endlichen Dehnungen ausgesetzt werden zu können, wird die Theorie für große Dehnungen unter Verwendung logarithmischer Dehnungen zusammen mit der aktualisierten Lagrange-Formel für dieses Modell benutzt.

Das konstitutive Modell wird also konstruiert, um die logarithmischen Dehnungen und die Kirchhoffschen Spannungskomponenten miteinander in Beziehung zu setzen. Schließlich werden die konstitutive Matrix und der Spannungsvektor jedoch transformiert, um die (wahren) Cauchy-Spannungen zu liefern.

sst1, sft1=Anfangs- und Endfließspannung für Zugbelastung. [SIGT_S1, SIGT_F1]

sst2, sft2=Anfangs- und Endfließspannung für Zugentlastung. [SIGT_S2, SIGT_F2]

ssc1, sfc1=Anfangs- und Endfließspannung für Druckbelastung. [SIGC_S1, SIGC_F1]

ssc2, sfc2=Anfangs- und Endfließspannung für Druckentlastung. [SIGC_S2, SIGC_F2]

eul = (Maximale plastische Zugdehnung)(3/2)0.5

Für die exponentielle Fließregel werden die zusätzlichen Eingabekonstanten bt1, bt2, bc1, und bc2 verwendet:

bt1 = Materialparameter, misst die Geschwindigkeit der Transformation für Zugbelastung, [BETAT_1]

bt2 = Materialparameter, misst die Geschwindigkeit der Transformation für Zugentlastung, [BETAT_2]

bc1 = Materialparameter, misst die Geschwindigkeit der Transformation für Druckbelastung, [BETAC_1]

bc2 = Materialparameter, misst die Geschwindigkeit der Transformation für Druckentlastung, [BETAC_2]

Das Fließkriterium

Zum Modellieren der Wahrscheinlichkeit der Druckabhängigkeit der Phasentransformation wird eine Belastungsfunktion vom Typ „Drucker-Prager“ für das Fließkriterium verwendet:

 F(t) =\/2 s + 3 a p

 F- Rif = 0

Dabei gilt Folgendes:

s = Wirkspannung

p = Mittelspannung (oder hydrostatischer Druck)

a = \/(2/3) ( ssc1- sst1) / ( ssc1+ sst1)

Rfi = [ sfi( \/(2/3) + a )] : i = 1: Belastung, i = 2: Entlastung

Die Fließregel

Durch Übernahme der logarithmischen Dehnungsdefinition können die deviatorischen und volumetrischen Komponenten der Dehnungs- und Spannungstensoren und ihre Beziehungen korrekt in einer entkoppelten Form ausgedrückt werden.

Zuerst werden die plastischen und elastischen Gesamtdehnungsvektoren betrachtet, die durch folgende Gleichungen dargestellt werden:

ep = eul xs ( n + a m )

ee = e  - ep

Damit kann der Kirchhoffsche Spannungsvektor folgendermaßen berechnet werden:

t = pm + t

p = K ( q - 3 a eulxs)

t = 2G ( e - eul xs n)

In den obigen Formeln gilt Folgendes:

eul = skalarer Parameter, der die maximale plastische Materialdehnungsverformung [EUL] darstellt

xs = Parameter zwischen 0 und 1, als Maß der plastischen Dehnung

q =  volumetrische Dehnung = e11 + e22 + e33

e = deviatorischer Dehnungsvektor

t= deviatorischer Spannungsvektor

n = Norm der deviatorischen Spannung: t/(\/2s) ?

m = die Identitätsmatrix in Vektorform: {1,1,1,0,0,0}T

K bzw. G = der elastische Kompressions- bzw. Schubmodul: { K = E/[3(1-2n), G = E/[2(1+v)]}

Die lineare Fließregel in der inkrementellen Form kann dementsprechend wie folgt ausgedrückt werden:

Laden: Dxs= ( 1,0 - xs)DF / ( F - R1f)

Entlastung: Dxs= xs DF / ( F - R2f)

Sowie der exponentielle Durchflusswert (Fließregel), wenn ein b ungleich Null definiert ist:

Laden: Dxs= b1( 1,0 - xs)DF / ( F - R1f)2

Entlastung: Dxs= b2xs DF / ( F - R2f)2

Hinweise:

• Im Allgemeinen hängen Formgedächtnislegierungen nicht von Geschwindigkeitseffekten ab. Daher stellt die „Zeit“ in der obigen Formel eine Pseudovariable dar, und ihre Größe wirkt sich nicht auf die Lösung aus.

• Alle Gleichungen sind hier für Zugbelastungen bzw. Zugentlastungen dargestellt. Ähnliche Ausdrücke (mit Druckeigenschaftsparametern) können für die Druckbelastungs- bzw. Druckentlastungsbedingungen verwendet werden.

• Beim inkrementellen Lösungsalgorithmus wird hier ein Rückabbildungsverfahren in der Berechnung von Spannungen und konstitutiven Gleichungen für einen Lösungsschritt verwendet. Die Lösung besteht demnach aus zwei Teilen. Zuerst wird ein Testzustand berechnet. Wenn der Testzustand das Fließkriterium verletzt, wird eine Anpassung zur Rückgabe der Spannungen an die Fließoberfläche vorgenommen.

Verweise:

1. Auricchio, F., „A Robust Integration-Algorithm for a Finite-Strain Shape-Memory-Alloy Superelastic Model“, International Journal of Plasticity, Band 17, S. 971-990, 2001.

2. Auricchio, F.,  Taylor, R.L., and Lubliner, J., „Shape-Memory-Alloys: Macromodeling and Numerical Simulations of the Superelastic Behavior“, Computer Methods in Applied Mechanics and Engineering, Band 146, S. 281-312, 1997.

3. Bergan, P.G., Bathe, K.J., and Wunderlich, eds. „On Large Strain Elasto-Plastic and Creep Analysis“, Finite Elements Methods for Nonlinear Problems, Springer-Verlag 1985.

4. Hughes, T., eds. „Numerical Implementation of Constitutive Models: Rate-Independent Deviatoric Plasticity“, Theoretical Foundation for Large-Scale Computations for Nonlinear Material Behavior, Martinus Nijhoff Publishers, Dordrecht, The Netherlands, 1984.