減衰効果（Damping Effects）
動的システムに初期条件を適用すると、システムは動きが止まるまで減少する振幅で振動します。 この現象は減衰（damping）と呼ばれます。 減衰（damping）はエネルギーが様々な減衰メカニズム（例えば内部摩擦、外部摩擦、微小レベルの周期弾性ひずみ材料における熱の影響、空気抵抗など）により消費される複雑な現象です。
散逸メカニズムを数式で表すことは困難であり、 減衰効果は一般的に理想化された数学的定式で表現されます。 多くの場合、減衰効果は粘性減衰によって十分に表現することができます。
粘性減衰（あるいはダッシュポット）は速度に比例した力を生成します。 粘性流体（油など）で満たされた円筒形内で自由に動くピストンなどが粘性減衰の例と言えます。 減衰力（Fd）は減衰の2つの端点における相対速度に対して線形とされます。
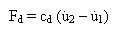(関係式 1)
定数 cd （つまり、Fd vs 相対速度のカーブの傾き）は粘性減衰係数（coefficient of viscous damping）と呼ばれます:
粘性減衰係数の単位は（力）/（速度）（(force)/(velocity)）あるいは（力x時間）/（長さ）（(force x time)/(length)）です。
粘性減衰（n-自由度）システムの応答は次により与えられます:
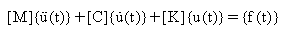(関係式 2), ここで:
[M] = n x n 対称質量（あるいは慣性）マトリックス
[C] = n x n 対称減衰マトリックス
[K] = n x n 対称剛性マトリックス
{f(t)} = n-次元力ベクトル
, 
, 
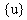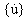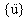はそれぞれ変位、速度、加速度（n-次元ベクトル）です。
一般的に、古典的なモーダル解析（modal analysis）は、モーダル座標変換の結果である減衰行列（[c]）が対角行列として扱われない限り、必ずしも独立した運動方程式につながるわけではありません。
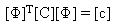(関係式 3)
以下の種類の減衰が利用可能です:
関連トピック
モーダル時刻歴解析（Modal Time History Analysis）
調和解析（Harmonic Analysis）
不規則振動解析（Random Vibration Analysis）