平均応力補正（Mean Stress Correction）
応力周期に対する交番応力の振幅は、周期内の応力範囲の1/2で計算されます。 応力周期を原因とする損傷量は、交番応力のみに依存するのではなく、平均応力にも依存します。 たとえば、下記の2つの周期は同一の交番応力を有していますが、平均応力が異なるため、異なる損傷量が生じます。
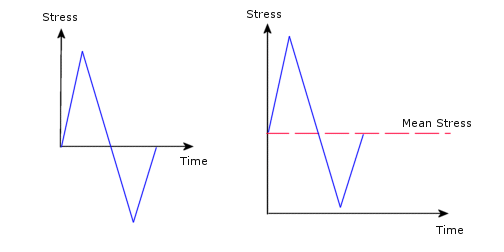
周期上にある平均応力の損傷に対する影響は、以下のダイアグラム（Haigh ダイアグラム）により説明されます。
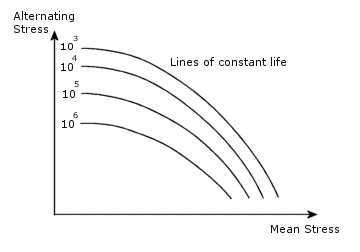
平均応力は、荷重が完全可逆である場合のみゼロになります。 最も簡単なケースは、同一の R 比による S-N カーブが荷重として与えられる場合です。 この場合の S-N カーブは補正を必要としないため、直接的に使用されます。 異なる R 比により S-N カーブを定義した場合、ソフトウェアはカーブ間の線形補間により平均応力を考慮します。 荷重の R 比と異なる R 比による S-N カーブが 1 つだけ提供される場合には、補正が必要となります。
プログラムは、平均応力の計算に常に von Mises 応力を使用します。 Von Mises は、正の結果量のため、関連する平均応力を計算する目的で最大平均主応力のマークが割り当てられます。
定義（Definitions）
補正手法を説明するにあたり、応力周期に対して以下の変数を定義します：
Smax = 最大応力
Smax = 最小応力
DS = 応力範囲 = Smax- Smin
Sa = 交番応力 = (Smax - Smin)/2
Smean = 平均応力 = (Smax + Smin)/2
R = 応力比 = Smin/Smax
A = 振幅比 = Sa/Smean
一般的な荷重に対する応力比および振幅比を以下に示します：
|
荷重タイプ |
応力および振幅比 |
|
完全な反転 |
R = -1、A = 無限 |
|
ゼロから最大 |
R = 0、A = 1 |
|
ゼロから最小 |
R = 無限、A = 1 |
補正手法（Correction methods ）
以下において：
Sca = 補正済み交番応力（ゼロ平均に基づいて）、
Sy = 降伏応力、および
Su = 極限応力
ソフトウェアは、Sca の計算に以下の手法を提供します：
|
手法 |
方程式 |
|
1. Goodman 手法 - 一般的に脆性材料に適しています。 |
|
|
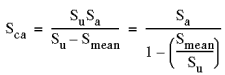
2. Gerber 手法 - 一般的に延性材料に適しています。 |
|
|
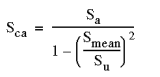
3. Soderberg 手法 - 一般的に最も無難な手法です。 |
|
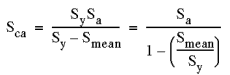
変動および一定振幅イベントの双方に対して、ソフトウェアは各周期の交番応力に加えて平均応力を計算し、指定条件を用いた補正済み応力の評価を行います。
関連トピック
定義（Definitions）
一定振幅疲労イベントからの交番応力評価（Evaluation of Alternating Stresses From Constant Amplitude Fatigue Events）
疲労解析の実行（Performing Fatigue Analysis）
S-N カーブ（S-N Curve）
疲労プロット（Fatigue Plot）