線性彈力同向模型

若材料的屬性不會因方向而改變，即可稱之為等向性材料。因此，等向性材料於所有方向上的彈性模數、Poisson 比、熱膨脹係數及熱傳導率等一概相同。等溫一詞有時也用來指稱熱膨脹係數無特定方向性的材料。

要定義等向彈力屬性，必須定義彈性模數 E x。 x00a0;如果您未 x00a0;指定任何特定值，程式會假設 Poisson 比 n xy 的值為 0.0。 x00a0;常用的 Poisson 比值是 0.3。即使已明確指定剪力模數 G xy，程式仍會執行內部運算。

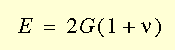
等向性材料的勁度矩陣僅含有兩個獨立的係數。下節說明在包含熱應變效應的二維及三維空間中的等向性應力-應變關係。

等向性應力-應變關係

包含熱效應的等向性應力-應變關係最常見的形式如下圖所示：

線性彈性材料模型假定

線性彈性材料模型的假定條件如下：

• 線性假定。所引起的反應是與所套用的負載力直接成比例的。例如，如果您將負載力的值加倍，則模型的反應 (位移、應變、及應力) 也會加倍。在滿足下列條件的情況下，您可以做出線性假定。

• 最高應力位在自原點起成一直線的應力-應變曲線之線性範圍內。隨著應力增加，材料會顯現出高於特定應力位階的非線性行為。此項假定主張應力應低於此位階。某些材料 (例如橡膠) 即使在低應力下亦會顯現出非線性的應力-應變關係。

• 最大位移遠小於模型的特性尺寸。例如，板的最大位移必須遠遠小於其厚度，橫樑的最大位移也必須遠遠小於其橫截面的最小尺寸。

• 彈性假定。不會造成任何永久性變形的負載量。換句話說，假設模型具有絕對彈性。具有絕對彈性的模型在負載解除後會回復其原有的形狀。

等向及正交材料