Модели текучести
Ползучестью называется зависимая от времени деформация, возникающая в состоянии постоянной нагрузки. Ползучесть наблюдается в большинстве материалов для проектирования, особенно в металлах при повышенных температурах, высокомолекулярных полимерных пластмассах, бетоне и твердом ракетном топливе. В связи с достаточно большим периодом времени развития, эффекты ползучести не принимаются в расчет при динамических анализах.
Диаграммой ползучести является график деформации-времени. Для диаграммы ползучести, различаются три режима: первичный, вторичный и третичный (см. рис. ниже) В основном, рассматриваются первичный и вторичный режимы.
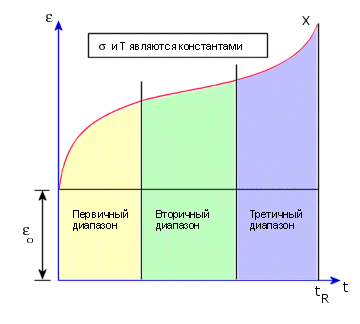
Применяются два положения ползучести, основанные на "Уравнении состояния" Каждое правило определяет выражение для неосевой деформации ползучести, в виде значений неосевой нагрузки и времени.
Классический закон ползучести (правило Bailey-Norton)

где:
T = Температура (Кельвин) (= исходная температура + справочная температура + температура смещения)
C
T = A постоянная материала, определяющая температурную зависимость ползучести
C0 — это постоянная текучести 1, которая указана на вкладке Свойства диалогового окна Материал.
Единицы постоянной текучести 1 должны указываться в системе СИ. Коэффициент преобразования равен 1/ (напряжение ^ (C1) * время^(C2)). Единицы напряжения указываются в Н/м2 , а время в секундах.
C1 — это постоянная текучести 2, а C2 — постоянная текучестви 3 в диалоговом окне свойств материала.
Классический закон ползучести описывает первичный и вторичный режимы ползучести в одной формуле. Третичный режим ползучести не рассматривается. “t” является текущим действительным (не псевдо-) временем, s - суммарное неосевое напряжение в момент времени t.
Для применения данных правил к параметрам многоосевой ползучести, были сделаны следующие предположения:
-
Правило неосевой ползучести является действительным, при замене параметра неосевой деформации ползучести и неосевого напряжения соответствующими эффективными значениями.
-
Материал является изотропным
-
Деформации ползучести являются несжимаемыми
Для числового анализа ползучести, с возможностью применения циклической нагрузки, основываясь на правиле деформационного отверждения, текущие параметры деформации ползучести выражаются в виде функции текущей нагрузки и суммарной деформации ползучести:

где:
