Wann ist eine dynamische Analyse durchzuführen?

Bei statischen Studien wird angenommen, dass Lasten konstant sind oder sehr langsam angewendet werden, bis ihre volle Stärke erreicht ist. Aufgrund dieser Annahme wird davon ausgegangen, dass Geschwindigkeit und Beschleunigung der einzelnen Partikel des Modells gleich Null sind. Folglich werden Trägheits- und Dämpfungskräfte in statischen Studien ignoriert.

In der Praxis werden Lasten oft nicht langsam angewendet, oder sie ändern sich in Abhängigkeit von der Zeit oder Frequenz. Verwenden Sie in solchen Fällen eine dynamische Studie. Im Allgemeinen sollte eine dynamische Studie verwendet werden, wenn die Frequenz einer Last größer als 1/3 der tiefsten Frequenz (Grundfrequenz) ist.

Lineare dynamische Studien basieren auf Frequenzstudien. Die Software berechnet die Reaktion des Modells durch Summierung des Beitrags aller Schwingungen zur Lastumgebung. In den meisten Fällen liefern nur die unteren Schwingungen einen bedeutenden Beitrag zur Reaktion. Der Beitrag einer Schwingung hängt vom Frequenzanteil sowie der Größe, Richtung, Dauer und Position der Last ab.

Die Ziele einer dynamischen Analyse sind:

• Konstruktion von strukturellen und mechanischen Systemen, die fehlerlos in einer dynamischen Umgebung funktionieren

• Modifizierung von Systemmerkmalen (Geometrie, Dämpfungsmechanismus, Materialeigenschaften usw.) zur Verminderung von Vibrationseffekten

Bewegungsgleichungen

Einfreiheitsgradsysteme (SDOF-Systeme)

Betrachten Sie das einfache Massefedersystem. Die Masse (m) wird einer Kraft F(t) in Richtung u als Funktion der Zeit ausgesetzt. Die Masse kann sich nur in Richtung u bewegen. Daher handelt es sich hier um ein Einfreiheitsgradsystem (SDOF). Der Bewegung wird durch eine Feder der Steifigkeit (k) Widerstand geleistet.

.

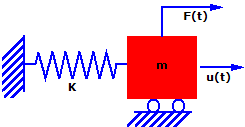
Wenn für dieses System zum Zeitpunkt (t) das zweite newtonsche Gesetz (Kraft = Masse mal Beschleunigung) angewendet wird, ergibt sich Folgendes:

F(t)-ku(t) = mu..(t)

oder

mu..(t) + ku(t) = F(t)

Bedeutung:

u..(t) ist die Beschleunigung der Masse zum Zeitpunkt (t) und entspricht in Bezug auf die Zeit der zweiten Ableitung von u

k = Steifigkeit der Feder

Theoretisch vibriert die Masse, wenn sie verschoben und losgelassen wird, unendlich mit der gleichen Amplitude. Praktisch vibriert die Masse in immer kleineren Amplituden, bis sie zum Stillstand kommt. Dieses Phänomen wird als Dämpfung bezeichnet, die durch einen Energieverlust aufgrund von Reibung und anderen Effekten verursacht wird. Dämpfung ist ein komplexes Phänomen. Hier wird von der Annahme ausgegangen, dass die Dämpfungskraft proportional zur Geschwindigkeit ist. Dieser Dämpfungstyp wird als viskose Dämpfung bezeichnet.

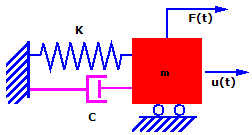
Unter Berücksichtigung der Dämpfung lautet die obige Gleichung wie folgt:

mu..(t) + cu.(t) + ku(t) = F(t)

Bedeutung:

u..(t) ist die Beschleunigung der Masse zum Zeitpunkt (t) und entspricht in Bezug auf die Zeit der ersten Ableitung von u

Anmerkung: In statischen Studien sind Geschwindigkeit und Beschleunigung so gering, dass sie vernachlässigbar sind, und F und u sind keine Funktionen der Zeit. Die obige Gleichung reduziert sich auf F=ku.

Mehrfreiheitsgradsysteme (MDOF-Systeme)

Bei einem Mehrfreiheitsgradsystem (MDOF) werden m, c und k zu Matrizen (anstelle von Einzelwerten). Die Bewegungsgleichungen werden wie folgt ausgedrückt:

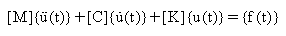. Dabei gilt Folgendes:

[M]: Massenmatrix

[K]: Steifigkeits-Matrix

[C]: Dämpfungsmatrix

{u(t)}: Verschiebungsvektor zum Zeitpunkt t (Verschiebungskomponenten der einzelnen Knoten)

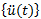Beschleunigungsvektor zum Zeitpunkt t (Beschleunigungskomponenten der einzelnen Knoten)

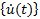Geschwindigkeitsvektor zum Zeitpunkt t (Geschwindigkeitskomponenten der einzelnen Knoten)

{f(t)}: zeitabhängiger Lastvektor (Kraftkomponenten der einzelnen Knoten)

Siehe auch

Lineare statische Analyse versus lineare dynamische Analyse

Dynamische Lasten

Lasten und Ergebnisoptionen für dynamische Analysen