Grundkonzepte der Analyse
Die Software verwendet die Finite-Elemente-Methode (FEM). FEM ist ein numerisches Verfahren für die Analyse von technischen Konstruktionen. FEM ist aufgrund der Allgemeingültigkeit und Eignung für die Computerimplementierung als Standard-Analysemethode anerkannt. FEM unterteilt das Modell in viele kleine Teile mit einfachen Formen, die als Elemente bezeichnet werden, und ersetzt auf effektive Art und Weise ein komplexes Problem durch viele einfache Probleme, die simultan gelöst werden müssen.
|

|

|
|
CAD-Modell eines Teils
|
In kleine Teile (Elemente) unterteiltes Modell
|
Die Elemente haben gemeinsame Punkte, die als Knoten bezeichnet werden. Das Verfahren der Unterteilung des Modells in kleine Teile nennt man Vernetzung.
Das Verhalten jedes Elements unter allen möglichen Trag- und Lastszenarien ist bekannt. Die Finite-Elemente-Methode verwendet Elemente mit verschiedenen Formen.
Die Reaktion an jedem Punkt in einem Element wird ausgehend von der Reaktion der Elementknoten berechnet. Jeder Knoten ist in vollem Umfang durch eine Reihe von Parametern definiert, die von der Analyseart und dem verwendeten Element abhängig sind. So beschreibt beispielsweise die Temperatur eines Knotens in vollem Umfang dessen Reaktion bei einer thermischen Analyse. Bei strukturellen Analysen wird die Reaktion eines Knotens im Allgemeinen durch drei Translationen und drei Rotationen beschrieben. Diese werden als Freiheitsgrade bezeichnet. Die Analyse unter Verwendung der Finite-Elemente-Methode wird Finite-Elemente-Analyse (FEA) genannt.
|
|
|
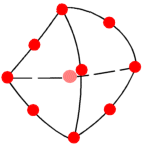
Ein tetraedrisches Element. Die roten Punkte stellen Knoten dar. Die Kanten eines Elements können abgerundet oder gerade sein.
|
Die Software erstellt die Gleichungen, die das Verhalten der einzelnen Elemente regeln; dabei werden auch die Verbindungen der Elemente untereinander berücksichtigt. Diese Gleichungen setzen die Reaktion mit bekannten Materialeigenschaften, Lager und Lasten in Verbindung.
Anschließend gliedert das Programm die Gleichungen in einen großen Satz simultaner algebraischer Gleichungen und ermittelt die Unbekannten.
Bei einer Spannungsanalyse beispielsweise ermittelt der Gleichungslöser die Verschiebungen an jedem Knoten. Das Programm errechnet anschließend daraus die entsprechenden Dehnungen und Spannungen.
Die Software bietet die folgenden Studientypen (Analysearten) an:
-
Statische Studien (oder Spannungsstudien). Statische Studien berechnen Verschiebungen, Reaktionskräfte, Dehnungen, Spannungen und die Verteilung des Sicherheitsfaktors. Das Material versagt an den Stellen, an denen die Spannungen ein gewisses Maß überschreiten. Die Berechnung des Sicherheitsfaktors basiert auf einem von vier Versagenskriterien.
Statische Studien können Sie dabei unterstützen, ein Versagen aufgrund zu hoher Spannungen zu vermeiden. Ein geringerer Sicherheitsfaktor als Eins weist auf ein Versagen des Materials hin. Große Sicherheitsfaktoren in einem zusammenhängenden Bereich zeigen geringe Spannungen an, so dass Sie im entsprechenden Bereich wahrscheinlich Materialeinsparungen vornehmen können.
-
Frequenzstudien. Ein in seinem Beharrungszustand gestörter Körper neigt bei bestimmten Frequenzen, die als Eigenfrequenzen oder Resonanzfrequenzen bezeichnet werden, zu Vibrationen. Die geringste Eigenfrequenz wird als Grundfrequenz bezeichnet. Für jede Eigenfrequenz nimmt der Körper eine gewisse Form an, die als Schwingungsform oder Eigenform bezeichnet wird. Die Frequenzanalyse berechnet die Eigenfrequenzen und die dazugehörigen Schwingungsformen.
Theoretisch verfügt ein Körper über eine unendliche Zahl von Schwingungsformen. Bei der Finite-Elemente-Analyse (FEA) gibt es theoretisch genauso viele Schwingungsformen wie Freiheitsgrade (DOFs). In den meisten Fällen werden nur ein paar Schwingungsformen berücksichtigt.
Eine übermäßige Reaktion tritt auf, wenn ein Körper einer dynamischen Last ausgesetzt wird, die in einer seiner Eigenfrequenzen vibriert. Dieses Phänomen wird als Resonanz bezeichnet. So schlingert beispielsweise ein Auto mit einem nicht ausgewuchteten Reifen aufgrund dieser Resonanz bei gewissen Geschwindigkeiten. Das Schlingern nimmt bei anderen Geschwindigkeiten ab oder verschwindet gänzlich. Ein weiteres Beispiel ist ein starker Klang, wie etwa die Stimme eines Opernsängers, die ein Glas zum Zerspringen bringen kann.
Die Frequenzanalyse kann Sie dabei unterstützen, ein Versagen aufgrund von übermäßigen, durch Resonanz hervorgerufenen Spannungen zu vermeiden. Außerdem bietet sie Informationen zur Lösung dynamischer Reaktionsprobleme.
Lineare dynamische Studien basieren auf Frequenzstudien. Die Software berechnet die Reaktion des Modells durch Summierung des Beitrags aller Schwingungen zur Lastumgebung. In den meisten Fällen liefern nur die unteren Schwingungen einen bedeutenden Beitrag zur Reaktion. Der Beitrag einer Schwingung hängt vom Frequenzanteil sowie der Größe, Richtung, Dauer und Position der Last ab.
Die Ziele einer dynamischen Analyse sind: (a) die Konstruktion von strukturellen und mechanischen Systemen, die fehlerlos in einer dynamischen Umgebung funktionieren, und (b) die Reduktion von Vibrationseffekten.
-
Knicken. Knickanalysen (Beulanalysen). Knicken bezieht sich auf plötzliche große Verschiebungen aufgrund axialer Lasten. Schwache Strukturen, die axialen Lasten ausgesetzt werden, können bereits bei einer Last knicken bzw. versagen, die unterhalb der Last liegt, die zu einem Materialversagen führt. Knicken kann in verschiedenen Formen unter der Wirkung verschiedener Lasten auftreten. In vielen Fällen ist nur die geringste Knicklast von Interesse.
Knickstudien können Sie dabei unterstützen, ein Versagen aufgrund von Knicken zu vermeiden.
-
Thermisch. Thermische Analysen. Thermische Studien berechnen Temperaturen, Temperaturgradienten und den Wärmestrom auf der Grundlage der Wärmeerzeugung, der Wärmeleitung, der Konvektion und der Wärmestrahlung. Thermische Studien können Ihnen helfen, unerwünschte thermische Bedingungen wie etwa Überhitzung und Schmelzen zu vermeiden.
-
Konstruktionsstudien
. Optimierungskonstruktionsstudien automatisieren die Suche nach der optimalen Konstruktion auf der Grundlage einer geometrischen Konstruktion. Die Software ist mit einer Technologie zur schnellen Erkennung von Tendenzen und zur Ermittlung der optimalen Lösung bei kleinstmöglicher Anzahl von Programmzyklen ausgestattet. Optimierungskonstruktionsstudien erfordern die Definition der folgenden Parameter:
-
-
Ziele. Geben Sie das Ziel der Studien an. Ein Ziel wäre beispielsweise der Mindestmaterialaufwand.
-
Konstruktionsvariablen. Wählen Sie die Bemaßungen aus, die sich ändern dürfen, und legen Sie Grenzwerte fest. So kann beispielsweise der Durchmesser einer Bohrung von 0,5 Zoll bis 1,0 Zoll variieren, während die lineare Austragung einer Skizze zwischen 2,0 Zoll und 3,0 Zoll variieren kann.
-
Zwangsbedingungen. Legen Sie die Bedingungen fest, die von der optimalen Konstruktion erfüllt werden müssen. Sie können beispielsweise festlegen, dass eine Spannungskomponente einen bestimmten Wert nicht übersteigt und dass die Eigenfrequenz in einem festgelegten Bereich liegt.
ANMERKUNG: Für Nicht-Optimierungskonstruktionsstudien definieren Sie keine Ziele.
-
Nicht-lineare
Studien. Wenn die Annahmen der linearen statischen Analyse nicht gültig sind, können Sie das Problem mit nicht-linearen Studien lösen. Die Hauptquellen der Nichtlinearität sind: große Verschiebungen, nicht-lineare Materialeigenschaften und Kontakt. Nicht-lineare Studien berechnen Verschiebungen, Reaktionskräfte, Dehnungen und Spannungen zu unterschiedlichen Last- und Lagerinkrementen. Wenn Trägheits- und Dämpfungskräfte nicht ignoriert werden können, können Sie nicht-lineare dynamische Analyse verwenden.
 Nicht-lineare Studien beziehen sich auf nicht-lineare strukturelle Studien. Bei thermischen Studien löst die Software automatisch ein lineares oder nicht-lineares Problem auf Grundlage der Materialeigenschaften sowie thermischer Lager und Lasten.
Nicht-lineare Studien beziehen sich auf nicht-lineare strukturelle Studien. Bei thermischen Studien löst die Software automatisch ein lineares oder nicht-lineares Problem auf Grundlage der Materialeigenschaften sowie thermischer Lager und Lasten.
Das Lösen eines nicht-linearen Problems ist weitaus zeitintensiver und erfordert mehr Ressourcen als das Lösen einer vergleichbaren linearen statischen Studie.
Das Prinzip der Überlagerung gilt nicht bei nicht-linearen Studien. Wenn beispielsweise die Anwendung der Kraft F1 an einem Punkt die Spannung S1 verursacht und die Kraft F2 die Spannung S2, verursacht die gemeinsame Anwendung beider Kräfte NICHT zwangsläufig die Spannung (S1+S2) an dem Punkt, wie dies bei linearen Studien der Fall ist.
Nicht-lineare Studien helfen Ihnen bei der Überprüfung des Verhaltens einer Konstruktion über die Beschränkungen von statischen Studien und Knickstudien hinaus.
 Statische Studien bieten eine nicht-lineare Lösung von Kontaktproblemen, wenn Sie die Option Große Verschiebung aktivieren.
Statische Studien bieten eine nicht-lineare Lösung von Kontaktproblemen, wenn Sie die Option Große Verschiebung aktivieren.
-
Fallprüfung. Fallprüfungsanalysen. Fallprüfungsstudien bewerten die Auswirkungen, die beim Aufprall einer Konstruktion auf einen starren Boden entstehen. Neben der Schwerkraft können Sie die Fallhöhe oder die Geschwindigkeit zum Zeitpunkt des Aufpralls festlegen. Das Programm löst ein dynamisches Problem als eine Zeitfunktion unter Verwendung expliziter Integrationsmethoden. Explizite Methoden sind zwar schnell, erfordern jedoch die Verwendung kleiner Zeitinkremente. Aufgrund der großen Menge an Informationen, die die Analyse erzeugen kann, speichert das Programm die Ergebnisse an bestimmten Zeitpunkten und Positionen, die vor der Ausführung der Analyse festgelegt wurden.
Nach Abschluss der Analyse können Sie Verschiebungen, Geschwindigkeiten, Beschleunigungen, Dehnungen und Spannungen grafisch darstellen.
-
Ermüdung. Ermüdungsanalysen. Das wiederholte Belasten führt im Laufe der Zeit zu einer Schwächung der Objekte, selbst wenn die induzierten Spannungen weit unter den zulässigen Spannungsgrenzen liegen. Die Anzahl der Zyklen, die erforderlich sind, damit ein Versagen aufgrund von Ermüdung an einer bestimmten Stelle eintritt, hängt vom Material und den Spannungsschwankungen ab. Diese materialspezifischen Informationen liefert die Wöhlerkurve. Sie stellt die Anzahl der Zyklen, die einen Fehler verursachen, für verschiedene Spannungsstärken dar. Mit Ermüdungsstudien wird die Lebensspanne eines Objekts aufgrund von Ermüdungsereignissen und Wöhlerkurven ermittelt.