動解析を使用するとき（When to Use Dynamic Analysis）
静解析では、荷重が一定かまたは完全な値に到達するまでに非常に時間をかけて適用されるものとして見なされます。この仮定により、モデルにおける全ての位置で速度と加速度もゼロと見なされます。結果として、静解析スタディは慣性力と減衰力を無視したものとなります。
実用的なケースで、荷重をゆっくりと適用できなかったり、時間や固有値とともに変化する場合が多くあります。このような場合に動的スタディを使用します。一般的に、荷重の固有値が最小固有値（基本固有値）の 1/3 より大きい場合には、動的解析スタディを使用します。
線形動解析スタディは固有値解析スタディに基づいたものです。ソフトウェアは、それぞれのモードの影響を荷重環境に累積することにより、モデルの応答を計算します。ほとんどの場合、低いモードのみが応答に対して顕著に影響を与えます。モードの影響は、荷重の固有値内容、大きさ、方向、所要時間、および位置に依存します。
動解析の目的には次が含まれます:
運動方程式（Equations of Motion）
1自由度系（Single Degree of Freedom (SDOF) Systems）
簡単なスプリング質量系について考えてみます。質量 (m) は 時間の関数として、U方向にF(t) の力が作用します。質量は u 方向にのみ移動できるため、1自由度系（Single-Degree-Of-Freedom (SDOF) system）と呼びます。運動はスプリングの剛性 (k) による抵抗力が作用します。
.
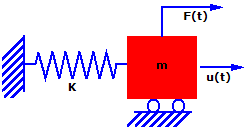
この系のニュートンの第2法則（力=質量x加速度）を時間(t)の関数で表すと：
F(t)-ku(t) = mu..(t)
または
mu..(t) + ku(t) = F(t)
ここで、
u..(t) は時間 (t) における質量の加速度であり、時間に対して u の2次導関数に等しい
k = スプリングの剛性
論理的には、質量が変位し解放された場合は、質量は同じ振幅でいつまでも振動を続けることになります。実際には、質量は動きが止まるまで減少する振幅で振動します。この現象を減衰と呼びます。これは摩擦やその他の作用でエネルギーが消費されるために起こります。減衰は複雑な現象です。ここでは、減衰効果が速度に比例するとします。この種類の減衰は粘性減衰（viscous damping）と呼びます。
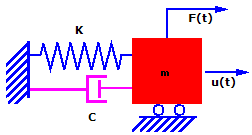
減衰効果を考慮すると上記の式は次のようになります:
mu..(t) + cu.(t) + ku(t) = F(t)
ここで、
u.(t) は時間 (t) における質量の速度であり、時間に対して u の1次導関数に等しい
注記:静解析スタディでは、速度と加速度は微々たるものとして無視され、F と u は時間の関数とされません。上記の式は次のようになります:F=ku
多自由度系（Multi Degree of Freedom (MDOF) Systems）
多自由度系、m、c、k は単一の値ではなく行列となり、運動方程式は次のようになります:
ここで、
[M]:質量マトリックス
[K] :剛性マトリックス
[C] :減衰マトリックス
{u(t)}:時間 t における変位ベクトル（各節点における変位）
時間 t における加速度ベクトル（各節点における加速度）
時間 t における速度ベクトル（各節点における速度）
{f(t)}:時変荷重ベクトル（各節点における力）
関連トピック
線形静解析 vs 線形動解析（Linear Static Versus Linear Dynamic Analysis）
動的荷重
動解析の荷重と結果オプション（Loads and Result Options for Dynamic Analysis）