가소성 von Mises 모델
항복 기준은 다음과 같이 정의할 수 있습니다.
여기에서 s는 유효 응력이고 s
Y는 단축 테스트에서의 항복 응력입니다. von Mises 모델을 사용하여 금속의 동작을 설명할 수 있습니다. 이런 재질 모델을 사용할 때 다음을 고려해야 합니다.
변수 RK가 동역학 및 등방성 가공경화의 균형을 정의합니다.
등방성 가공경화만일 경우, 변수 RK의 값은 0입니다. 항복 곡면의 반경이 확장되나 편차 공간에서 중심이 고정됩니다.
동역학 가공경화만일 경우, 변수 RK의 값은 1입니다. 편차 공간에서 중심이 이동할 수 있으나 항복 곡면의 반경이 일정합니다.
-
가소성에 대한 평형
또는 다중 선형 단축 응력-변형 곡선을 입력할 수 있습니다. 평형 응력-변형 곡선 정의의 경우, 항복 응력과 탄성 계수는 재질 대화 상자에서 입력할 수 있습니다. 다중 선형 응력-변형 곡선 정의일 경우 응력-변형 곡선을 정의해야 합니다.
-
응력-변형 곡선을 정의할 때 곡선의 첫 번째 지점이 재질의 항복 지점이어야 합니다. 탄성 계수, 항복 응력 등과 같은 물성치는 응력-변형 곡선을 사용할 수 있는 경우 이 곡선에서 가져오며 재질 대화 상자의 물성치 테이블에서 가져오지 않습니다. 포아송비(NUXY)만 이 테이블에서 가져옵니다.
응력-변형 곡선 정의는 낙하 충격 해석 스터디에서는 지원되지 않습니다.
Huber-von Mises 모델을 솔리드(시험 품질 및 고품질)와 두꺼운 쉘 요소(시험 품질 및 고품질)와 함께 사용할 수 있습니다.
열가소성은 쉘 요소에는 사용할 수 없습니다.
다음 그림은 플라스틱 재질의 전형적인 응력-변형 곡선입니다.
대변형 해석
대변형 가소성 이론에서 대수 변형 측정은 다음과 같이 정의됩니다.
여기서 U는 대체로 변형 구배 F(예 F = R U, R은 회전 텐서)의 정확한 극 분해에서 얻은 정확한 늘이기 텐서입니다. 증분 대수 변형은 다음과 같이 대략적으로 계산됩니다.
여기서 B
(n+1/2)는 n+1/2 시간 단계에서 계산된 변형률-변위 매트릭스이고 D
u는 증분형 변위 벡터입니다. 앞의 공식은 정확한 공식에 근접한 2차 근사값입니다.
응력 비율은 Green-Naghdi 비율로 사용되므로 구성 모델을 정확한 프레임의 불변량 또는 목적 계수로 만듭니다. 전체 시스템의 응력 비율을 R-시스템으로 변환
전체 구성 모델은 형태적으로 소변형 이론과 동일합니다. 대변형 가소성 이론은 von Mises 항복 기준, 관련 유동 규칙 및 등방성 또는 동역학 가공경화(평행 또는 다중 선형)에 적용됩니다. 물성치의 온도 의존성은 평행 가공경화에 지원됩니다. 현재 경우에 방사형 반환 알고리듬을 사용할 수 있습니다. 기본 개념은 다음으로 법선 벡터의 대략적인 값을 구하는 것입니다.
여기서
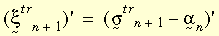
다음 그림은 위의 두 수식을 설명합니다.
요소 힘 벡터 및 경사도 매트릭스는 업데이트된 라그랑주 공식을 기준으로 계산됩니다. 코쉬 응력, 대수 변형 및 현재 두께(쉘 요소에만 해당)은 출력 파일에 기록됩니다.
현재 경우의 탄성은 작은 탄성 변형은 있지만 임의의 더 큰 소성 변형을 허용한다는 가정으로 hyperelastic 형태로 모델링됩니다. 대변형 탄성 문제(고무 등)일 경우 Mooney-Rivlin과 같은 hyperelastic 재질 모델을 사용할 수 있습니다.
코쉬(실제 크기) 응력 및 대수 변형을 사용하여 다중 선형 응력-변형 곡선을 정의해야 합니다.
가소성에 대한 Tresca 및 von Mises 기준 비교