隨時間變化的力量所激發的線性 n 自由度系統的動作方程式系統為：
(方程式 1)
使用座標轉換，n 個聯立方程式集減少至 n 個獨立方程式 (每個方程式可以獨立解出)：
r = 1、2、....、n (方程式 2)
其中 xr(t) 是形式座標，藉由以下方程式與節點座標 ur(t) 關聯：
(方程式 3)。
形式負載的向量 {m(t)} 的計算公式如下：
(方程式 4)。
假設激振是由其功率頻譜密度 (psd) 函數所表示，求解可以在頻率域中用公式表示。如果激振 psd 矩陣給定為 [Sf(ω)] 提供，形式力 psd 矩陣會定義為：
(方程式 5)。
形式位移回應的 psd [Sx(ω)] 是自下列方程式得出：
(方程式 6)，
其中 [H(ω)] 是形式轉移函數矩陣，而 [H*(ω)] 則是其共軛複數。若為正常模式，轉移函數矩陣與對角元素 Hr(ω) 成對角。
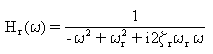(方程式 7) 和
(方程式 8)。
位移回應 psd [Su(ω)] 隨即導出 (方程式 3)。
(方程式 9)。
速度與加速度回應的 psd 是由以下方程式表示：
(方程式 10)，和
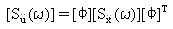(方程式 11)。
形式速度與加速度 psd 是透過以下方程式與形式位移 psd 關聯：
(方程式 12)，和
(方程式 13)
方程式 10 和方程式 11 可以重寫成：
(方程式 14) 和 
(方程式 15)。
形式回應 psd 的零延遲形式自動相關性回應 (τ=0) 是透過以下整數計算：
(方程式 16)
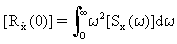(方程式 17)
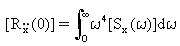(方程式 18)。
從以上的方程式可以看出，均方回應是由矩陣的對角項所決定：
(方程式 19)，
(方程式 20)，
(方程式 21)。
應力均方回應
元素應力 {σ} 是透過節點位移 {u} 由下列決定：
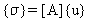(方程式 22)，或以下列的形式位移 {x}：
(方程式 23)，其中 [Φ] 是特徵向量的矩陣。
應力相關性矩陣 [Rσ] 的計算公式如下：
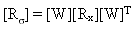(方程式 24)。