Elastické materiály se schopností odvádět mechanickou energii díky účinkům viskozity se označují jako viskózně elastické.
Pro stav víceosého napětí lze základní vztah zapsat takto:
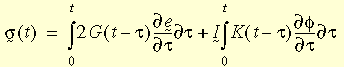
kde: e(bar) a φ představují výchylkové a objemové namáhání, G(t - τ) a K(t - τ) jsou funkce smyku a uvolnění objemové pružnosti.
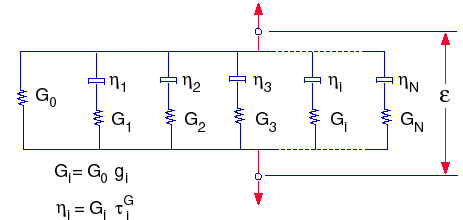
Funkce uvolnění pružnosti může poté zastupovat mechanický model, kterému se obvykle říká zobecněný Maxwellův model s výrazy:
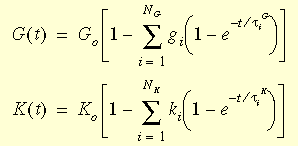
kde: G0 = E / 2(1+ ν), počáteční modul pružnosti (t=0)
a K0 = E / 3(1 -2ν), počáteční objemový modul (t=0)
gi, ki, τiG a τiK jsou i-té smykové a objemové moduly a odpovídající časy.
Účinek teploty na chování materiálu je prezentován pomocí vztahu času a teploty. Matematická forma principu je tato:
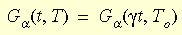
kde γt je snížený čas a γ je funkce posunu. Funkci přibližně zpracovává rovnice WLF (Williams-Landel-Ferry):
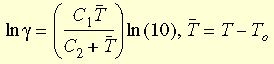
kde T0 je referenční teplota, která se obvykle získá jako teplota přechodu na sklovitost; C1 a C2 jsou konstanty závislé na materiálu.
| Parametr |
Vlastnosti materiálu |
|---|
| Lineární elastické parametry |
Modul pružnosti v X |
| Poissonova konstanta v XY |
| Modul pružnosti ve smyku v XY |
| Parametry funkce uvolnění |
Modul uvolnění ve smyku (1 až 8) (představuje g1, g2, ...,g8 v rovnicích zobecněného Maxwellova modelu)
|
| Časové hodnoty (Modul uvolnění ve smyku 1 až 8) (představuje τ1g, τ2g,..., τ8g v rovnících zobecněného Maxwellova modelu) |
| Modul uvolnění objemové pružnosti (1 až 8) |
| Časové hodnoty (Modul uvolnění objemové pružnosti 1 až 8) (představuje τ1k, τ2k,..., τ8k v rovnících zobecněného Maxwellova modelu) |
| Parametry rovnice WLF
|
Teplota přechodu na sklovitost (představuje T0 v rovnici WLF)
|
| První konstanta pro rovnici Williams-Landel-Ferry (představuje C1 v rovnici WLF)
|
| Druhá konstanta pro rovnici Williams-Landel-Ferry (představuje C2 v rovnici WLF)
|
Při definování křivky uvolnění ve smyku nebo uvolnění objemové pružnosti na záložce Tabulky a křivky je první bod křivky modul G1 nebo K1 v čase t1. V čase t = 0 program automaticky vypočítá G0 nebo K0 z modulu pružnosti a Poissonovy konstanty.
Viskózně elastický model materiálu lze použít u objemových elementů a elementů s širokou skořepinou v nízké i vysoké kvalitě.