| VON |
von Mises 응력 |
| P1 |
수직 응력 (최대 주응력) |
| P2 |
수직 응력 (중간 주응력) |
| P3 |
수직 응력 (최소 주응력) |
| INT |
응력 강도 = P1-P3 (a) P1: 최대 절대 수직 응력, P3: 최소 절대 수직 응력.
|
| TRI |
3축 응력 = P1 + P2 + P3(주요 응력 요소의 합계입니다. 또한 첫 응력 불변량이라고도 하는데 값이 응력 텐서에 어떤 좌표 변환을 적용해도 바뀌지 않기 때문입니다.) |
| SX 값 |
선택한 참조 형상의 X 방향 수직 응력 |
| SY 값 |
선택한 참조 형상의 Y 방향 수직 응력 |
| SZ |
선택한 참조 형상의 Z 방향 수직 응력 |
| TXY |
선택한 참조 형상의 YZ 평면에 작용하는 Y 방향 전단 응력 |
| TXZ |
선택한 참조 형상의 YZ 평면에 작용하는 Z 방향 전단 응력 |
| TYZ |
선택한 참조 형상의 XZ 평면에 작용하는 Z 방향 전단 응력 |
| ERR |
Energy Norm Error(에너지 놈의 오차) |
| CP |
접촉 압력(b) |
| ILTXZ |
XZ 평면의 층간 전단 |
| ILTYZ |
YZ 평면의 층간 전단 |
(a) 일부 설계 코드와 참조 자료에서는 Tresca 상당 응력이 (P1 – P3)과 같은 최대 전단 응력의 두 배로 정의되거나 응력 강도로 정의됩니다.
(b) 접촉 압력은 좌표 변환에 의한 전체 절점 응력에서 파생됩니다. 솔버가 각 절점에서의 접촉 하중을 보고합니다. 접촉 하중 방향의 단위 벡터 N이 전체 좌표계의 {Nx, Ny, Nz}일 경우 접촉 압력 {Px, Py, Pz}의 세 요소를 전체 좌표계에서 파생시키기 위해 절점 응력 텐서가 단위 벡터 N을 따라 투영됩니다.
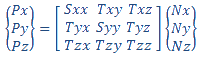
각 절점에서의 접촉 압력 CP의 크기는 각 요소 제곱의 합의 제곱근입니다. 접촉 압력의 방향은 항상 접촉 영역에 수직입니다.
