W badaniach drgań losowych wykorzystywane są niżej wymienione metody całkowania.
Metoda standardowa
Metoda standardowa analizy drgań losowych przebiega następująco:
-
Wybierane są pewne punkty częstotliwości wokół każdego modu drgań własnych. Lokalizacje tych punktów zależą od wartości parametru bias p.
Dla parametru bias równego 1.0, wszystkie punkty częstotliwości są jednorodnie rozłożone pomiędzy częstotliwościami drgań własnych. Jeżeli parametr bias jest większy od 1.0, wybierane punkty leżą bliżej częstotliwości drgań własnych. Domyślne wartości dla punktów częstotliwości oraz parametru bias są funkcją stosunku tłumienia pierwszego modu ζ. Aby zapoznać się ze sposobem wybierania punktów częstotliwości, kliknąć tutaj.
Poniżej podano domyślne wartości dla punktów częstotliwości oraz parametru bias w funkcji ζ:
| Modalny stosunek tłumienia
|
Liczba częstotliwości (domyślna)
|
Parametr bias (domyślny)
|
|---|
| ζ < 0,01
|
21 |
11
|
| 0,01 < ζ < 0,1 |
21-4,34 cala (ζ /0,01)
|
11-3,47 cala (ζ /0,01)
|
| ζ > 0,1
|
11
|
3
|
Oprogramowanie stosuje wartości domyślne podane w Tabeli 1, gdy zero (0) jest zdefiniowane zarówno dla Liczby punktów częstotliwości, jak i Parametru bias.
- Modalne gęstości widmowe mocy (PSD) są oszacowywane w każdym punktu częstotliwości. Limit stosunku dla dowolnych dwóch częstotliwości (RATIO) określa limit stosunku wszystkich możliwych par częstotliwości drgań własnych (wi / wj, i > j).
Oznacza to, że dla każdej pary modów, gdzie wi / wj > RATIO, warunki gęstości międzywidmowej są pomijane. Efekty międzymodalne nie są rozważane dla RATIO = 1.
- Modalne gęstości widmowe mocy (PSD) są następnie całkowane numerycznie w określonym zakresie częstotliwości, aby uzyskać wartości średniokwadratowe i kowariancje reakcji modalnej. Całkowanie wykonywane jest metodami numerycznymi z wykorzystaniem całkowania Gaussa 2 lub 3 w każdym interwale częstotliwości, w oparciu o interpolację logarytmiczną. Reakcja średniokwadratowa uzyskiwana jest poprzez sumowanie udziałów interwałów.
- Na końcu przekształcenie wielkości modalnych na węzłowe pozwala uzyskać średniokwadratowe przemieszczenia, prędkości i przyspieszenia układu.
Metoda przybliżona
Standardowe metody całkowania mogą być czasochłonne ze względu na całkowanie numeryczne dużych macierzy. Metoda przybliżona całkowania dokonuje uproszczonego rozwiązania z zastosowaniem następujących założeń:
- Pominięcie reakcji międzymodalnej, Sx(ω), która jest skutkiem oddziaływania jednego modu na inny, tj.
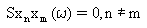(Równanie 1)
- Gęstości widmowe mocy (PSD) wzbudzeń są uznawane za stałe wokół każdego modu. Zatem zakłada się, że każdy mod jest wzbudzany przez „biały szum” o gęstości widmowej Sn, gdzie:
(Równanie 2)
ωn jest częstotliwością drgań własnych modu n (n = 1, 2, ...nf).
Dla białego szumu reakcje średniokwadratowe można określić analitycznie dla reakcji modalnych:
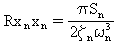(Równanie 3)
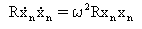(Równanie 4)
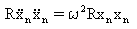(Równanie 5).