Sistemas de un grado de libertad (SDOF)
Considere el sistema sencillo de resorte de masa. La masa (m) está sujeta a una fuerza F(t) en la dirección u como una función del tiempo. Sólo se permite que la masa se mueva en la dirección u y, por tanto, éste es un sistema de un grado de libertad (SDOF). Un resorte de rigidez (k) resiste el movimiento
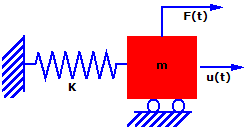
Si escribimos la segunda ley de Newton (fuerza es igual a masa por aceleración) para este sistema en el momento (t) da como resultado:
F(t)-ku(t) = mu..(t)
o:
mu..(t) + ku(t) = F(t)
donde:
u..(t) es la aceleración de la masa en el momento (t) y es igual a la segunda derivada de u con respecto al tiempo
k = es la rigidez del resorte
En teoría, si la masa se desplaza y se suelta, continuará vibrando con la misma amplitud. Sin embargo, en la práctica, la masa vibra con amplitudes progresivamente más pequeñas hasta que se detiene. Este fenómeno se denomina amortiguamiento y está originado por una pérdida de energía mediante fricción y otros efectos. El amortiguamiento es un fenómeno complejo. Para los fines de esta explicación, suponemos que la fuerza de amortiguamiento es proporcional a la velocidad. Este tipo de amortiguamiento se llama amortiguamiento viscoso.
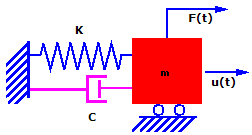
Si tenemos en cuenta el amortiguamiento, la ecuación anterior se convierte en:
mu..(t) + cu.(t) + ku(t) = F(t)
donde:
u.(t) es la velocidad de la masa en el momento (t) y es igual a la primera derivada de u con respecto al tiempo
En estudios estáticos, la velocidad y aceleración son tan pequeñas que pueden despreciarse, y F y u no son funciones del tiempo. La ecuación se reduce a: F=ku.
Sistemas de múltiples grados de libertad (MDOF)
Para un sistema de múltiples grados de libertad (MDOF), m, c y k son matrices en lugar de valores únicos, y las ecuaciones de movimiento se expresan así:
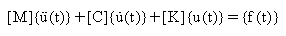
donde:
[M]: matriz de masa
[K] : matriz de rigidez
[C] : matriz de amortiguamiento
{u(t)}: vector de desplazamiento en el momento t (componentes de desplazamiento de cada nodo)
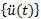: vector de aceleración en el momento t (componentes de aceleración de cada nodo)
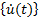: vector de velocidad en el momento t (componentes de velocidad de cada nodo)
{f(t)}: vector de carga dependiente del tiempo (componentes de fuerza de cada nodo)