U dílu, na který působí opakované cyklické zatížení o určité frekvenci nebo náhodné vibrace, můžete předvídat míru jeho poškození a zbývající dobu životnosti.
K dispozici pro aplikaci SOLIDWORKS Simulation Premium.
Nástroj umožňuje provádět únavovou analýzu na základě událostí ve frekvenční doméně, které využívají výsledků studií lineárních dynamických harmonických a náhodných vibrací.
Výsledkem únavové studie na základě událostí ve frekvenční doméně je zbývající doba životnosti a nákresy poškození. V případě únavových studií vycházejících z náhodných vibrací jde též o graf Doba do prasknutí.
Výsledky únavové studie vycházející z výsledků harmonické studie
Únavová studie, která vychází z výsledných napětí jako funkce frekvence z lineární dynamické harmonické studie, předpovídá zbývající dobu životnosti a poškození dílů, na který působí pravidelné (nebo sinusové) vibrace po zadaný počet cyklů při určité pracovní frekvenci.
Výpočet koeficientu kumulativního poškození je vychází z pravidla lineárního poškození neboli Minerova pravidla:
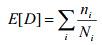
kde E [D] je předpokládaný koeficient poškození, nI je počet cyklů, kterým je díl vystaven při určité pracovní frekvenci a střídavém napětí SI a NI je počet cyklů nutných k tomu, aby došlo k prasknutí při napětí SI podle křivky S-N daného materiálu.
Únavová studie vycházející z výsledků studie náhodných vibrací
Je-li třeba odhadnout únavu materiálu v případech, kdy vývoj napětí nebo namáhání v rámci konstrukce nebo součásti má náhodný charakter (a pro jeho popis je tedy nejvhodnější použít statistické parametry jako hustotu pravděpodobnosti, počet průchodů nulou směrem vzhůru nebo počet špiček za sekundu), jsou k dispozici následující výpočetní metody frekvenční domény:
- Úzkopásmová metoda
- Steinbergova metoda
- Wirschingova metoda
Prognóza únavy materiálu na základě frekvence vychází z předpokladu, že parametry odezvy (napětí a namáhání) analyzovaného modelu jsou náhodné a statické a odpovídají Gaussovu rozdělení.
Na rozdíl od jiných únavových studií je křivka S-N daného materiálu definována Basquinovou rovnicí:
N = B / (Se )m
kde N = přípustný počet cyklů do prasknutí, B = konstanta specifická pro danou křivku (průsečík s osou S), Se = rozsah napětí cyklického zatížení, m = sklon lineární části křivky S-N.
Tato rovnice ukazuje, že při cyklickém zatížení s konstantní amplitudou existuje lineární vztah mezi počtem cyklů do prasknutí dílu N a působícím rozsahem napětí Se, jestliže tyto parametry vykreslíme s použitím logaritmických stupnic.