바디에 하중이 가해질 때, 바디는 보통 여러 곳에 걸친 분산 내력을 일으켜 그 효과를 받아들입니다. 이러한 물체 속에 생기는 저항력의 강도를 응력이라고 합니다. 응력의 단위는 단위 면적당 힘입니다.
응력의 분력
막대에 압력을 가한다고 가정해 봅니다. P점에서의 응력 상태는 임의의 평면을 기준으로 표현될 수 있습니다. 합력은 항상 같다 하더라도 응력의 분력 값은 선택한 평면에 따라 다릅니다.
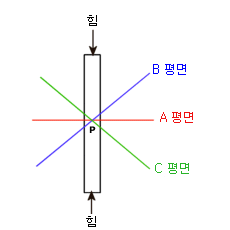
응력은 크기, 방향, 작용 평면에 의해 정의됩니다. 특정 위치에서의 응력의 상태는 다음 분력 요소로 완전히 정의될 수 있습니다.
|
SX
|
YZ-평면에 수직으로 작용하는 X-방향 응력
|
|
SY
|
XZ-평면에 수직으로 작용하는 Y-방향 응력
|
|
SZ
|
XY-평면에 수직으로 작용하는 Z-방향 응력
|
|
TXY
|
X-방향에 수직인 평면(YZ-평면)에 작용하는 Y-방향 응력
|
|
TYX
|
Y-방향에 수직인 평면(XZ 평면)에 작용하는 X-방향 응력
|
|
TXZ
|
X-방향에 수직인 평면(YZ-평면)에 작용하는 Z-방향 응력
|
|
TZX
|
Z-방향에 수직인 평면(XY-평면)에 작용하는 X-방향 응력
|
|
TYZ
|
Y-방향에 수직인 평면(XZ-평면)에 작용하는 Z-방향 응력
|
|
TZY
|
Z-방향에 수직인 평면(XY-평면)에 작용하는 Y-방향 응력
|
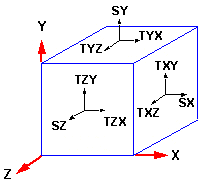
SX, SY, SZ를 수직 응력이라 하고 TXY, ...., TZY를 전단 응력이라고 합니다. 전단 응력은 다음 수식으로 연관됩니다: TXY = TYX, TXZ = TZX, TYZ = TZY. 따라서 특정 위치에서의 응력 상태는 이 여섯 개의 분력으로 완전 정의됩니다.
주응력
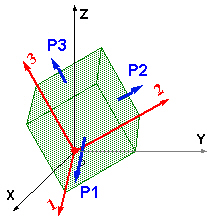
각 점에서, 전단 응력이 없는 평면이 있습니다. 이 평면에 대한 응력의 상태는 주응력이라는 수직 응력으로 완전 정의됩니다.
|
P1
|
첫 번째 주 방향의 수직 응력(최대)
|
|
P2
|
두 번째 주 방향의 수직 응력(중간)
|
|
P3
|
세 번째 주 방향의 수직 응력(최저)
|
|
|
상당 응력(von Mises 응력라고도 함)
SimulationXpress에서 해당 (또는 von Mises) 응력이라고 하는 응력을 보게 됩니다. 특정 위치에서의 상당 응력이 해당 위치에서의 응력 상태를 유일하게 나타내는 것은 아니지만 여러 연성 재질에 대한 안전도를 평가하는데 적절한 정보를 제공해 줍니다.
응력 부품과는 달리 유효 응력에는 방향이 없습니다. 유효 응력은 응력 단위와 함께 크기로 완전 정의됩니다. 다른 위치에서의 안전계수를 계산하기 위해 SimulationXpress는 유효 응력이 재질의 항복 강도에 이르렀을 때 특정 위치에서 항복을 시작하는 기준을 정의하는 von Mises 항복 기준(Yield Criterion)을 사용합니다.