비선형 동적 해석의 경우, 비선형 정적 해석과 같이 사용되는 절차: 제어, 반복과 종료의 순서입니다.
비선형 동적 해석에서, 시간 간격이 t+Δt인 동적 시스템의 평형 방정식은 다음과 같습니다.
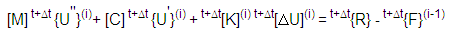
여기에서,
[M] = 시스템의 질량 행렬
[C] = 시스템의 댐핑 매트릭스
t+Δt[K](i) = 시스템의 강성 행렬
t+Δt{R} = 외부적으로 적용된 절점 하중의 벡터
t+Δt{F}(i-1) = 반복(i-1)에서 내부적으로 발생된 절점 힘의 벡터
t+Δt[ΔU](i) = 반복(i)에서의 증가 절점 변위 벡터
t+Δt{U}(i) = 반복(i)에서의 총 변위 벡터
t+Δt {U'}(i) = 반복 (i)에서의 총 속도 벡터
[M] t+Δt {U''}(i) = 반복 (i)에서의 총 가속도 벡터
Newmark-Beta이나 Wilson-Theta 방식과 같은 내연적 시간 적분 구조 사용과 Newton의 반복 방법을 사용해서 위의 수식이 양식에서 계산됩니다.
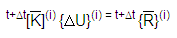
여기에서,
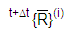 = 유효 하중 벡터
= 유효 하중 벡터
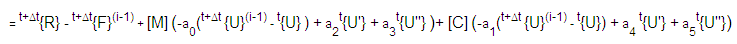
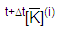 = 유효 강성 행렬 =t+Δt[K](i) + a0[M] + a1[C]
= 유효 강성 행렬 =t+Δt[K](i) + a0[M] + a1[C]
여기에서
0,
1,
2,
3,
4 및
5은(는) 내연적 적분 구조의 상수입니다.
- 하중 제어 증가 기술만이 비선형 동적 해석에 사용될 수 있습니다.
- 수정 Newton-Raphson(MNR) 및 Newton-Raphson(NR) 반복 구조를 비선형 동적 해석에 사용할 수 있습니다.