Упругие материалы, обладающие способностью рассеивания механической энергии из-за влияния вязкости, называются вязкоупругими материалами.
Для состояния многоосевого напряжения, уравнение состояния может быть представлено следующим образом:
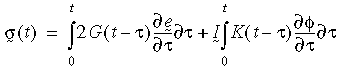
где: e(бар) и φ — девиаторная и объемная деформация, G(t - ) и K(t - ) – функции сдвига и общей релаксации.
Функции релаксации могут быть представлены механической моделью, известной как обобщенная модель Maxwell со следующими выражениями:

где: G0 = E / 2(1+ ν), исходный модуль сдвига (t=0)
и K0= E / 3(1 -2ν), исходный массовый модуль (t=0)
gi, ki, τi
G, and τi
K — модули i-того сдвига и общий модуль с соответствующими значениями времени.

Влияние температуры на поведение материала описывается, при помощи принципа соответствия времени-температуры. Ниже, представлено математическое выражение данного принципа:

где yt — сокращенное время и γ — функция смещения. Уравнение WLF (Williams-Landel-Ferry) используется, для приблизительного определения функции:

где T0 – справочная температура, обычно, называемой температурой перехода в прозрачное состояние; C1 и C2 – зависящие от материала постоянные.
| Параметр |
Свойства материала |
|---|
| Параметры линейной упругости |
Модуль упругости в X
|
|
Коэффициент Пуассона в XY
|
|
Модуль сдвига в XY
|
| Параметры функции релаксации |
Модуль релаксации при сдвиге (1 – 8) (представляют g1, g2,...,g8 в уравнениях обобщенной модели Maxwell)
|
|
Значения времени (Модуль расслабления при сдвиге от 1 до 8) (представляет τ1
g, τ2
g,..., τ8
g в уравнениях обобщенной модели Максвелла) |
|
Общий модуль релаксации (1 – 8) |
|
Значения времени (Модуль общего расслабления при сдвиге от 1 до 8) (представляет τ1
k, τ2
k,..., τ8
k в уравнениях обобщенной модели Максвелла) |
| Параметры уравнения WLF
|
Температура перехода в прозрачное состояние
(представляет T0 в уравнении WLF)
|
|
Первая постоянная для уравнения Вильямса-Ландела-Ферри (WLF)
(представляет C1 в уравнении WLF)
|
|
Вторая постоянная для уравнения Вильямса-Ландела-Ферри
(представляет C2 в уравнении WLF)
|
При определении кривой сдвига или общей релаксации на вкладке Таблицы и кривые первой точкой кривой является модуль G1 или K1 в момент времени t1. Для момента времени t = 0 программа автоматически вычисляет G0 или K0 из модуля упругости и коэффициента Пуассона.
Вязкоупругая модель материала может использоваться с твердотельными элементами и плотными оболочками низкого или высокого качества
При выполнении нелинейного анализа для вязкоупругой модели материала для отсчетов времени используются действительные числа.