| VON |
von Mises 응력 |
| VONDC: von Mises[방향 성분] |
선형 동적 - 조화 스터디에서만 사용 가능합니다. 솔버는 여섯 개 응력 요소의 적합한 기호(양수 또는 음수)를 고려하면서 von Mises 응력 계산을 보다 정확하게 수행합니다.
VON: Von Mises 응력 플롯은 6개 응력 성분에서 von Mises 응력을 계산합니다. VONDC: von Mises[방향 성분] 응력 플롯에서도 마찬가지입니다. 그러나 선형 동적 조화 스터디의 결과는 최대 정상 상태 진동 진폭에서 파생되기 때문에 von Mises 응력 결과의 기존 계산 방법은 응력 성분의 양수 값만 고려합니다. 특정 응력 성분이 양수지만, 다른 응력 성분이 인수인 경우 응력 단계 오프셋이 발생할 수 있습니다. VONDC: von Mises[방향 성분] 응력 플롯은 응력 단계 오프셋의 영향을 고려합니다. Von Mises 등식은 양수 응력 성분 값 사이의 차이와 비교했을 때 양수 응력 성분과 음수 응력 성분 간 차이의 제곱이 더 클 수 있음을 나타냅니다. 따라서 VONDC: von Mises[방향 성분] 응력 값은 VON: von Mises 응력 값보다 더 무난한 결과를 제공합니다.
|
| P1 |
수직 응력 (최대 주응력) |
| P2 |
수직 응력 (중간 주응력) |
| P3 |
수직 응력 (최소 주응력) |
| INT |
응력 강도 = P1-P3 (a)
P1: 최대 절대 수직 응력, P3: 최소 절대 수직 응력.
|
| TRI |
3축 응력 = P1 + P2 + P3(주요 응력 요소의 합계입니다. 또한 첫 응력 불변량이라고도 하는데, 값이 응력 텐서에 어떤 좌표 변환을 적용해도 바뀌지 않기 때문입니다.) |
| SX 값 |
선택한 참조 형상의 X 방향 수직 응력 |
| SY 값 |
선택한 참조 형상의 Y 방향 수직 응력 |
| SZ |
선택한 참조 형상의 Z 방향 수직 응력 |
| TXY |
선택한 참조 지오메트리의 X 방향에 수직인 평면에 작용하는 Y 방향 전단 응력 전단 응력 부품의 경우 첫 번째 지수는 곡면 수직 방향을 나타내고 두 번째 지수는 전단 응력 부품 방향을 나타냅니다.
|
| TXZ |
선택한 참조 지오메트리의 X 방향에 수직인 평면에 작용하는 Z 방향 전단 응력 |
| TYZ |
선택한 참조 지오메트리의 Y 방향에 수직인 평면에 작용하는 Z 방향 전단 응력 |
| ERR |
에너지 놈의 오차(정적 및 낙하/충격 테스트 스터디에서 사용 가능) |
| CP |
접촉 압력(b)
|
| ILTXZ |
XZ 평면의 층간 전단 |
| ILTYZ |
YZ 평면의 층간 전단 |

(a) 일부 설계 코드와 참조 자료에서는 Tresca 상당 응력이 (P1 – P3)과 같은 최대 전단 응력의 두 배로 정의되거나 응력 강도로 정의됩니다.
(b) 접촉 압력은 좌표 변환에 의한 전체 절점 응력에서 파생됩니다. 각 절점에서 솔버는 시뮬레이션 중에 나타날 수 있는 적용된 하중, 구속 조건, 접촉 하중이 작용하여 파생되는 접촉력을 보고합니다.
접촉 하중의 방향을 따라 단위 벡터 N은 전체 좌표계에서 {Nx, Ny, Nz}입니다. 절점 응력 텐서는 전체 좌표계에서 3개의 접촉력 성분 {Px, Py, Pz}를 유도하기 위해 단위 벡터 N을 따라 투영됩니다.
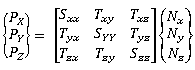
각 절점에서의 접촉 압력 CP의 크기는 각 요소 제곱의 합의 제곱근입니다. 접촉 압력의 방향은 항상 접촉 영역에 수직입니다.
