Zaman ile değişen bir kuvvet tarafından uyarılan doğrusal bir n serbestlik dereceli sistem için hareket denklemleri sistemi şu şekildedir:
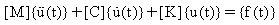 (Denklem 1)
(Denklem 1)
Koordinat dönüşümü kullanılarak n eşzamanlı denklemler seti, n bağımsız denklemlerine indirilir (her denklem bağımsız olarak çözülebilir):
 r = 1, 2, ...., n için (Denklem 2)
r = 1, 2, ...., n için (Denklem 2)
Burada xr(t), ur(t) düğüm koordinatlarıyla şu ilişkiye sahip modal koordinatlarıdır:
 (Denklem 3).
(Denklem 3).
Modal yükler vektörü {m(t)} şu şekilde hesaplanır:
 (Denklem 4).
(Denklem 4).
Uyarımların güç spektral yoğunluğu (psd) fonksiyonları ile ifade edildiğini varsayarsak çözüm, frekans etki alanında formüle edilebilir. Uyarım psd matrisi [Sf(ω)] olarak belirlenir, modal kuvvet psd matrisi şu şekilde tanımlanır:
 (Denklem 5).
(Denklem 5).
Modal yer değiştirme tepkisinin psd'si [Sx(ω)] şu şekilde elde edilir:
 (Denklem 6),
(Denklem 6),
Burada [H(ω)], modal aktarım fonksiyonu matrisidir ve [H*(ω)] bunun karmaşık eşleniğidir. Normal modlar için, aktarım fonksiyon matrisi diyagonal elemanlar içeren bir diyagonaldir Hr(ω)
 (Denklem 7) ve
(Denklem 7) ve
 (Denklem 8).
(Denklem 8).
Yer değiştirme tepkisi psd [Su(ω)], daha sonra (Denklem 3) kullanılarak türetilir.
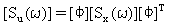 (Denklem 9).
(Denklem 9).
Hız ve ivme tepkilerinin psd'si şu şekilde ifade edilir:
 (Denklem 10) ve
(Denklem 10) ve
 (Denklem 11).
(Denklem 11).
Modal hız ve ivme psd'si, modal yer değiştirme psd'siyle şu ilişkiye sahiptir:
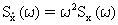 (Denklem 12) ve
(Denklem 12) ve  (Denklem 13)
(Denklem 13)
Denklem 10 ve Denklem 11 şu şekilde yeniden yazılabilir:
 (Denklem 14) ve
(Denklem 14) ve  (Denklem 15).
(Denklem 15).
Modal tepki psd'si açısından sıfır gecikme modal otomatik korelasyon tepkileri (τ=0) integrallerle hesaplanır:
 (Denklem 16)
(Denklem 16)
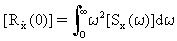 (Denklem 17)
(Denklem 17)
 (Denklem 18).
(Denklem 18).
Yukarıdaki denklemlerden; ortalama kare tepkileri, matrislerin diyagonal bileşenlerinden belirlenir:
 (Denklem 19),
(Denklem 19),
 (Denklem 20),
(Denklem 20),
 (Denklem 21).
(Denklem 21).
Gerilim Ortalama Kare Tepkisi
Eleman gerilimleri {σ}, şu şekilde düğüm yer değiştirmeleri {u} ile belirlenir:
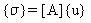 (Denklem 22) ya da modal yer değiştirmeleri {x} ile şu şekilde belirlenir:
(Denklem 22) ya da modal yer değiştirmeleri {x} ile şu şekilde belirlenir:
 (Denklem 23), burada [Φ] özvektörler matrisidir.
(Denklem 23), burada [Φ] özvektörler matrisidir.
Gerilim korelasyon matrisi [Rσ] şu şekilde belirlenir:
 (Denklem 24).
(Denklem 24).