Zaman ile değişen bir kuvvet tarafından uyarılan doğrusal bir n serbestlik dereceli sistemin hareket denklemleri sistemi şu şekildedir:
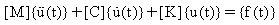 (Denklem 1)
(Denklem 1)
Burada;
[M] = n x n simetrik atalet matrisi
[C] = n x n simetrik sönümleme matrisi
[K] = n x n simetrik sertlik matrisi
{f(t)} = n boyutlu kuvvet vektörü
{u},  ve
ve  , sırasıyla yer değiştirme, hız ve ivme n boyutlu vektörleridir.
, sırasıyla yer değiştirme, hız ve ivme n boyutlu vektörleridir.
(Denklem 1), sabit katsayılara sahip n eşzamanlı adi diferansiyel denklemden oluşan bir sistemdir. Hareket denklemleri kütle, katılık ve sönümleme ifadeleri yoluyla ilişkilendirilir. İlişkilendirme, hareket denklemlerini matematiksel olarak tanımlamada kullanılan koordinat sistemine bağlıdır.
Modal analizdeki temel düşünce, modal matrisi [Φ] bir dönüşüm matrisi olarak kullanarak ilişkilendirilen (Denklem 1) sistemini bir dizi bağımsız denkleme dönüştürmektir. [Φ]; i = 1, ....,n için şu şekilde düzenlenen normal modları {f}i içerir:
 (Denklem 2)
(Denklem 2)
Sistemin normal modları ve özdeğerleri, özdeğer probleminin çözümünden türetilir:
 (Denklem 3)
(Denklem 3)
Burada [ω2], kareleri alınan doğal frekansların bir diyagonal matrisidir.
Doğrusal sistemler için n denklemli hareket sistemi, modal yer değiştirme vektörü {x} açısından n tek serbestlik dereceli denkleme ayrıştırılabilir:
 (Denklem 4)
(Denklem 4)
{u} vektörünün (Denk.4)'ten çıkarılması ve [Φ]T (Denklem 1) ile ön çarpımı şu sonucu verir:
 (Denklem 5)
(Denklem 5)
Normal modlar ortogonalite özelliğini karşılar ve modal matris [Φ] aşağıdaki denklemleri karşılayacak şekilde normalize edilir:
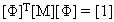 (Denklem 6)
(Denklem 6)
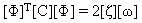 (Denklem 7) ve
(Denklem 7) ve
 (Denklem 8).
(Denklem 8).
(6--8 Denklemleri) çıkarıldığında, (Denklem 5) n bağımsız SDOF ikinci dereceden diferansiyel denklemli bir sisteme dönüşür:
 burada i =1, ..., n (Denklem 9)
burada i =1, ..., n (Denklem 9)
(Denklem 9); Wilson-Theta ve Newmark gibi adım adım integrasyon yöntemleri kullanılarak çözülür.
İntegrasyon, zaman etki alanında gerçekleştirilir. Burada, bir işlemden sonraki adımın sonuçlarını tahmin etmek için en son adımın sonuçlarını kullanılır.
Sistemin yer değiştirme vektörü (u), (Denklem 4)'ten türetilir.