Tek Serbestlik Dereceli (SDOF) Sistemler
Basit kütle-yay sistemini düşünün. Kütle (m), zamanın bir fonksiyonu olarak u yönünde bir kuvvete F(t) maruz kalır. Kütlenin sadece u yönünde hareket etmesine izin verilir ve dolayısıyla, bu Tek Serbestlik Dereceli (SDOF) bir sistemdir. Harekete, (k) sertliğinde bir yay direnç gösterir
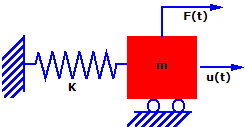
Bu sistem için (t) zamanında Newton'un İkinci Kanunu (kuvvet eşittir kütle çarpı ivme) yazıldığında şu ortaya çıkar:
F(t) - ku(t) = mu..(t)
veya
mu..(t) + ku(t) = F(t)
Burada;
u..(t), kütlenin (t) zamanındaki ivmesidir ve zamana göre u'nun ikinci türevine eşittir
k = yayın sertliğidir
Teorik olarak, kütlenin yeri değişirse ve serbest bırakılırsa daima aynı genlikte titremeye devam eder. Uygulamada, kütle dinlenme durumuna gelene kadar gittikçe azalan bir genlikle titrer. Bu olguya sönümleme denir ve sürtünme ve diğer etkiler yoluyla ortaya çıkan enerji kaybından kaynaklanmaktadır. Sönümleme karmaşık bir olgudur. Bu konuda sunulan açıklamalarda, sönümleme kuvvetinin hızla orantılı olduğunu varsayın. Bu sönümleme tipine visköz sönümleme denir.
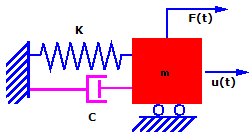
Sönümleme göz önünde bulundurulduğunda, yukarıdaki denklem şu hale gelir:
mu..(t) + cu.(t) + ku(t) = F(t)
Burada;
u.(t), kütlenin (t) zamanındaki hızıdır ve zamana göre u'nun birinci türevine eşittir
Statik etütlerde, hız ve ivme yok sayılabilecek kadar küçüktür ve F ile u, zamanın fonksiyonları değildir. Yukarıdaki denklem şuna indirgenir: F=ku.
Çok Serbestlik Dereceli (MDOF) Sistemler
Çok Serbestlik Dereceli (MDOF) bir sistem için m, c ve k tek değerler yerine matrislerdir ve hareket denklemleri şu şekilde ifade edilir:
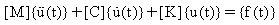
Burada;
[M]: kütle matrisi
[K]: sertlik matrisi
[C]: sönümleme matrisi
{u(t)}: t zamanındaki yer değiştirme vektörü (her düğümün yer değiştirme bileşenleri)
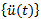 : t zamanındaki ivme vektörü (her düğümün ivme bileşenleri)
: t zamanındaki ivme vektörü (her düğümün ivme bileşenleri)
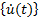 : t zamanındaki hız vektörü (her düğümün hız bileşenleri)
: t zamanındaki hız vektörü (her düğümün hız bileşenleri)
{f(t)}: zaman ile değişen yük vektörü (her düğümün kuvvet bileşenleri)