V lineární statické analýze se zatížení používají postupně a pomalu, dokud nedosáhnou plné velikosti. Po dosažení plné velikosti zůstávají konstantní (časově neměnné). Zrychlení a rychlosti buzeného systému jsou zanedbatelné, a proto ve formulaci nejsou brány v úvahu síly setrvačnosti a tlumení:

kde:
[K] : matice tuhosti
{u}: vektor posunutí
{f}: vektor zatížení
Výsledkem jsou konstantní napětí a posunutí.
V lineární dynamické analýze jsou použitá zatížení závislá na čase. Zatížení mohou být deterministická (periodická, neperiodická) nebo nedeterministická, což znamená, že je nelze přesně odhadnout, ale je možné je statisticky popsat. Zrychlení a rychlosti buzeného systému jsou značné, a proto jsou ve formulaci brány v úvahu síly setrvačnosti a tlumení:
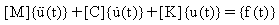
kde:
[K] : matice tuhosti
[C] : matice tlumení
[M]: matice hmoty
{u(t)}: časově proměnný vektor posunutí
 : časově proměnný vektor zrychlení
: časově proměnný vektor zrychlení
 : časově proměnný vektor rychlosti
: časově proměnný vektor rychlosti
{f(t)}: časově proměnný vektor zatížení
Reakce soustavy je dána v rámci průběhu (amplitudy v závislosti na čase) nebo v rámci frekvenčního spektra (špičkové hodnoty v závislosti na frekvenci).
U lineární dynamické analýzy se matice hmoty, tuhosti a tlumení s časem nemění.
Vlastnosti materiálů se považují za lineární. Pokud existuje nelinearita materiálu, je nutné použít nelineární dynamické studie.
Pokud je frekvence zatížení mnohem menší než nejmenší přirozená frekvence systému, je obecně možné předpokládat statické podmínky.