Soustava rovnic pohybu v lineárním systému s n stupni volnosti buzeném časově proměnnou silou je:
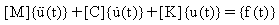(rovnice 1)
kde:
[M] = n x n symetrická matice setrvačnosti
[C] = n x n symetrická matice tlumení
[K] = n x n symetrická matice tuhosti
{f(t)} = n-rozměrný vektor síly
{u}, 
a 
jsou n-rozměrné vektory posunutí, rychlosti a zrychlení.
Rovnice 1 je soustava n souběžných diferenciálních rovnic s konstantními koeficienty. Rovnice pohybu jsou spojeny podmínkami hmotnosti, tuhosti a tlumení. Spojení závisí na souřadném systému, pomocí kterého byly rovnice pohybu matematicky popsány.
Základní myšlenkou modální analýzy je transformace spojené soustavy rovnic 1 do sady nezávislých rovnic pomocí modální matice [Φ] jako transformační matice. [Φ] obsahuje normální režimy {f}i pro i = 1, ....,uspořádané takto:
(rovnice 2)
Normální režimy a vlastní hodnoty (eigenvalues) systému jsou odvozeny z řešení problému vlastní hodnoty (eigenvalue):
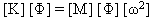(rovnice 3)
kde [w2] je druhá mocnina úhlopříčné matice přirozených frekvencí.
U lineárních systémů lze soustavu n rovnic pohybu rozložit na n rovnic s jedním stupněm volnosti na základě modálního vektoru posunutí {x}:
(rovnice 4)
Dosazením vztahu pro vektor {u} z rovnice 4 a vynásobením [Φ]T (rovnice 1) získáme:
(rovnice 5)
Normální režimy vyhovují vlastnosti ortogonality a modální matice [Φ] je normalizována, aby vyhovovala následujícím rovnicím:
(rovnice 6)
(rovnice 7) a
(rovnice 8).
Dosazením rovnic 6-8 se rovnice 5 stane soustavou n nezávislých SDOF diferenciálních rovnic druhého řádu:
pro i =1, ..., n (rovnice 9)
(Rovnice 9) se řeší pomocí metod integrace krok za krokem, například Wilson-Theta a Newmark.
Integrace se provádí v časové doméně, kde se pomocí výsledků posledního kroku odhadují výsledky dalšího kroku.
Vektor posunutí (u) je odvozen z rovnice 4.