Effets d'amortissement

Si vous appliquez des conditions initiales à un système dynamique, les système vibre à des amplitudes décroissantes jusqu'à ce que les vibrations cessent. Ce phénomène est appelé amortissement. L'amortissement est un phénomène complexe qui dissipe l'énergie au moyen de nombreux mécanismes tels que la friction interne et externe, les effets thermiques des matériaux subissant des déformations élastiques cycliques au niveau microscopique et la résistance de l'air.

Il est difficile de décrire les mécanismes de dissipation mathématiquement. Les effets d'amortissement sont généralement représentés par des formules mathématiques idéalisées. Dans de nombreux cas, les effets d'amortissement sont décrits adéquatement par des amortisseurs visqueux équivalents.

Un amortisseur visqueux (ou amortisseur d'oscillation) génère une force proportionnelle à la vitesse. Un piston pouvant se déplacer librement dans un cylindre rempli d'un fluide visqueux tel que l'huile est un exemple d'amortisseur visqueux. La force d'amortissement F_d est supposée être linéaire par rapport à la vitesse relative aux deux extrémités de l'amortisseur :

(Equation 1).

La constante c_d, qui représente la pente de la courbe F_d par rapport à la vitesse relative est appelée le coefficient d'amortissement visqueux ;

Les unités du coefficient d'amortissement visqueux sont (force)/(vitesse) ou (force x durée)/(longueur).

La réponse d'un système à n-degrés-de-liberté général subissant un amortissement visqueux est donnée par :

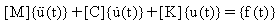(Equation 2)

où :

[M] = n x n matrice de masse (ou d'inertie) symétrique

[C] = n x n matrice d'amortissement symétrique

[K] = n x n matrice de raideur symétrique

{f(t)} = vecteur de force à n dimensions

{u}, et sont les vecteurs à n dimensions de déplacement, de vitesse et d'accélération, respectivement.

De manière générale, une analyse modale classique ne conduit pas nécessairement à un système d'équations de mouvement indépendant, à moins que la matrice d'amortissement [c] résultant de la transformation modale des coordonnées ne puisse être traitée comme une matrice diagonale.

(Equation 3)