Puisque l'emploi de Nitinol se justifie normalement par sa résistance à des déformations finies, ce modèle repose sur la théorie de grande déformation combinant les déformations logarithmiques et la formulation lagrangienne actualisée.
Le modèle constitutif est donc construit sur la base des déformations logarithmiques et des composantes de contrainte de Kirchhoff. Cependant, la matrice constitutive et le vecteur de contrainte sont en fin de compte transformés pour présenter les (vraies) contraintes de Cauchy.

|
σs
t1, σf
t1
|
Limite d'élasticité initiale et finale pour le chargement de traction [SIGT_S1, SIGT_F1]
|
|
σs
t2, σf
t2
|
Limite d'élasticité initiale et finale pour le déchargement de traction [SIGT_S2, SIGT_F2]
|
|
σs
c1, σf
c1
|
Limite d'élasticité initiale et finale pour le chargement de compression [SIGC_S1, SIGC_F1]
|
|
σs
c2, σf
c2
|
Limite d'élasticité initiale et finale pour le déchargement de compression [SIGC_S2, SIGC_F2]
|
|
eul
|
(Déformation plastique maximum en traction) *(3/2)0,5
|
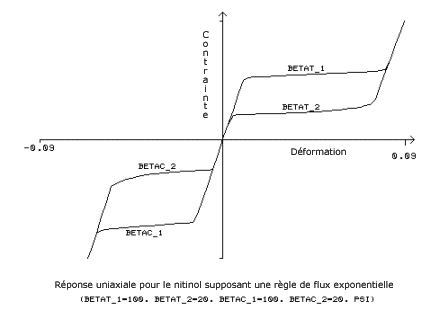
La règle de flux exponentielle utilise les contraintes d'entrée supplémentaires, β
t1, β
t2, β
c1, β
c2 :
|
βt1
|
paramètre de matériau, permettant de mesurer la vitesse de transformation pour le chargement de traction, [BETAT_1]
|
|
βt2
|
paramètre de matériau, permettant de mesurer la vitesse de transformation pour le déchargement de traction, [BETAT_2]
|
|
βc1
|
paramètre de matériau, permettant de mesurer la vitesse de transformation pour le chargement de compression, [BETAC_1]
|
|
βc2
|
paramètre de matériau, permettant de mesurer la vitesse de transformation pour le déchargement de compression, [BETAC_2]
|
Le critère d'élasticité
Afin de modéliser la dépendance potentielle de la pression par rapport au temps de la transformation de phase, une fonction de chargement de type Drucker-Prager est utilisée pour le critère d'élasticité :
F(τ) = sqrt(2)*σ(bar) + 3*α*p
F - RI
f = 0
où
σ(bar) = contrainte effective
p = contrainte moyenne (ou pression hydrostatique)
α = sqrt(2/3) (σsc1 - σst1 ) / (σsc1 + σst1)
Rf
I = [ σf
I(sqrt(2/3) + α)], I = 1 pour le chargement et 2 pour le déchargement