Finestra di dialogo Materiale - scheda Curve SN fatica

Utilizzare la scheda Curve SN fatica per definire le curve SN di uno studio di fatica. Le curve SN sono utilizzate solamente negli studi della fatica.

Origine

Per visualizzare questa finestra di dialogo:

Aprire una parte, fare clic con il pulsante destro del mouse su Materiale nell'albero di disegno FeatureManager e selezionare Modifica materiale.

La scheda Curve SN fatica è disponibile soltanto se è stato aggiunto SOLIDWORKS Simulation.

Per alcuni materiali della libreria dei materiali di SOLIDWORKS, le curve S-N di fatica sono già definite. Questi materiali sono identificati da un suffisso (S-N) applicato ai nomi nella libreria. Il riferimento per le curve SN è Atlas of Fatigue Curves, ASM International.

Imposta lo schema di interpolazione e l'origine dei dati.
Interpolare Imposta lo schema di interpolazione della sollecitazione alternata rispetto al numero di cicli della curva SN.
  • Log-log.

    Interpolazione logaritmica (base 10) del numero di cicli e sollecitazione alternata. Questa opzione è consigliata per le curve SN con pochi punti di dati ad ampia dispersione su entrambi gli assi, a meno che la curva non si adatti meglio con un altro schema di interpolazione.

  • Semi-log. Interpolazione lineare della sollecitazione e logaritmica per il numero dei cicli. Questa opzione è consigliata per le curve SN con intervalli di sollecitazione relativamente piccoli, rispetto alla variazione del numero di cicli, a meno che la curva non si adatti meglio con un altro schema di interpolazione.
  • Lineare. Interpolazione lineare sia della sollecitazione che del numero dei cicli. Questa opzione è consigliata per le curve SN con molti punti di dati, a meno che la curva non si adatti meglio con un altro schema di interpolazione

    Esempio di schemi di interpolazione SN

    in alcuni casi, la curva SN è disponibile sotto forma di equazione, ottenuta dall'ottimizzazione di dati sperimentali. In questi casi, se l'equazione coincide ad uno schema di interpolazione, potrebbe essere sufficiente definire solamente gli estremi della curva come punti di dati e utilizzare lo schema di interpolazione appropriato.
Definisci Definire manualmente i dati della curva. Selezionare fino a dieci curve nel menu.
Deriva dal modulo elastico del materiale Deriva automaticamente la curva SN sulla base delle curve SN ASME e dei moduli elastici del materiale di riferimento e di quello attivo. La curva SN di origine appare nell'Anteprima.
  • Basato su curve in acciaio Austenitico ASME
  • Basato su curve in acciaio al carbonio ASME

La curva SN risulta dalla divisione di ogni valore di sollecitazione della curva SN di riferimento per il modulo di elasticità del materiale ASME di riferimento, quindi moltiplicando questo risultato per il modulo di elasticità del materiale corrente. I numeri di cicli associati rimangono invariati.

Definire l'equazione S-N di fatica (per l'analisi della fatica relativa alla vibrazione casuale) Disponibile per gli studi di fatica basati sui risultati dagli studi di vibrazione casuale dinamica.

Dati di tabella

Elenca i dati della curva. Questi dati sono disponibili solo se nella casella Fonte è selezionato Definisci.
Rapporto sollecitazione (R) Disponibile solo quando Definito dall'utente è selezionato nella casella Seleziona fonte del materiale.
Unità Unità della Sollecitazione alternata.
se si immettono i valori, accertarsi di selezionare le unità di misura desiderate prima di specificare i valori.
Tabella dei dati curva Immettere a coppie i valori del numero di cicli e della sollecitazione alternata se si definisce manualmente la curva. Se la curva è derivata da una curva SN ASME di riferimento, appare la sua versione in scala.
È possibile utilizzare la tecnica Copia/Incolla per compilare la tabella.
Il file importa i dati della curva da un file. Disponibile solo quando Definito dall'utente è selezionato nella casella Seleziona fonte del materiale.
Vista Visualizza un grafico con i dati correnti della tabella.
Elimina Elimina la riga selezionata. Disponibile solo quando Definito dall'utente è selezionato nella casella Seleziona fonte del materiale.
Per applicare la stessa curva SN ai corpi con diversi materiali, nell'albero di studio della fatica fare clic con il tasto destro su Parti e selezionare Applica i dati di fatica a tutti i corpi.

Equazione della curva S-N (equazione di Basquin)

Disponibile per gli studi di fatica basati sui risultati dagli studi di vibrazione casuale dinamica lineare.

Stima costanti di Basquin dalla curva S-N Selezionare questa opzione per consentire al programma di calcolare le costanti dell'equazione di Basquin in base ai punti dati specificati della curva S-N.

Per l'alta resistenza alla fatica ciclica (numero di cicli N > 104), una curva S-N può essere approssimata da una linea retta se rappresentata in una scala log-log. L'equazione di Basquin è un rapporto di legge di potenza tra i cicli di sollecitazione applicati (S) nell'asse y e il numero di cicli necessari per provocare il cedimento (N) nell'asse y.

L'equazione di Basquin è valida solo fino al limite di resistenza o di fatica.
Il limite di resistenza è la sollecitazione alternata più alta e non comporta cedimenti per la fatica. In altre parole, se la sollecitazione alternata è uguale o più bassa del limite di resistenza, il numero dei cicli di sollecitazione per produrre il cedimento diventa molto grande (praticamente infinito). Il limite di resistenza è generalmente definito per le sollecitazioni alternate a media zero. Il limite di resistenza è anche noto come limite di fatica. Alcuni metalli non hanno un limite di resistenza misurabile.
Il programma considera i valori dell'intervallo di sollecitazione Sr per l'equazione di Basquin. Moltiplica per 2 i valori di sollecitazione alternata (Sa) della curva S-N per garantire un carico completamente invertito (Sr = 2*Sa).
L'equazione di Basquin sulla curva di fatica S-N è:
  • N = B / (Sr) m oppure
  • log (Sr) = B - m log (N)
Quando si seleziona questa opzione, le opzioni Costante specifica della curva (B) e Pendenza della curva S-N (m) sono disattivate. Il software calcola le costanti B e m adattando una linea retta tra i punti dati S-N utilizzando il metodo dei minimi quadrati di adattamento della linea. Queste costanti sono i parametri del materiale determinati tramite esperimenti di test di fatica con livelli di sollecitazione diversi.
Unità Imposta le unità per l'intervallo di sollecitazione Sr.
Considera il punto di taglio per la curva S-N alla riga Imposta il punto di taglio della curva S-N considerato per il calcolo delle costanti di Basquin. Se si immette 0 o 1, tutti i punti dati della curva S-N vengono considerati per l'adattamento di una linea retta utilizzando il metodo dei minimi quadrati di adattamento.
Se ad esempio si digita 4, il set di dati delle prime quattro righe della curva S-N viene considerato per l'adattamento di una linea retta e il calcolo delle costanti di Basquin B e m. È consigliabile utilizzare come punto di taglio il limite di resistenza alla fatica. La curva S-N viene considerata una linea orizzontale dopo il punto di taglio.
Costante specifica della curva (B) Immettere il valore (deve essere un numero reale positivo) per la costante B specifica della curva S-N. Si tratta del valore dell'intervallo di sollecitazione in un ciclo.
Pendenza della curva S-N (m) Immettere il valore della pendenza m della curva S-N (deve essere un numero intero positivo). Se si conoscono due punti dati, (N1, S1) e (N2, S2), la pendenza della curva S-N è data da: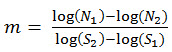
Origine Immettere le informazioni sulla fonte dei dati S-N.
Vista Selezionare questa opzione per visualizzare un grafico della curva S-N.
Salva Salva i dati della curva S-N in un file con formato *.dat o *.csv (delimitato da virgola).

Esempio di schemi di interpolazione SN

Si supponga di aver definito una curva SN con i seguenti due punti di dati consecutivi:
N. di cicli (N) Log (N) Sollecitazione alternata (S) Log (S)
1000 3 50.000 psi 4.699
100,000 5 40.000 psi 4.602
Al valore di sollecitazione 45.000 psi, il software importa il numero di cicli basati sullo schema di interpolazione SN seguente:
Curva SN log-log. L'asse X rappresenta il logaritmo del numero di cicli e l'asse Y la sollecitazione. Il software esegue l'interpolazione lineare sulla base del logaritmo di 45000 (ossia, 4,653). Con questa procedura, il numero di cicli risultante è 103,944 = 8.790.
Curva SN semi-log. L'asse X rappresenta il logaritmo del numero di cicli e l'asse Y la sollecitazione. Al valore di sollecitazione 45.000 psi, il software esegue l'interpolazione lineare e calcola il numero di cicli 104= 10.000.
Curva SN lineare. L'asse X rappresenta il numero di cicli e l'asse Y la sollecitazione. Al valore di sollecitazione 45.000 psi, il programma esegue l'interpolazione lineare e calcola il numero di cicli 50.500.