n x n 対称減衰マトリックス [C] は質量 [M] と剛性 [K] のマトリックスの線形結合として定式化されています:
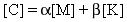(関係式 1)
-
アルファ係数 質量比例係数 α を設定します。
-
ベータ係数（Beta Coefficient）: 剛性比例係数 β を設定します。
(関係式 1) にある減衰タイプは Rayleigh （レイリー）減衰または比例減衰と呼ばれます。
[C] はシステム固有ベクトルに対して直交になります。
モーダル座標変換を適用することにより、モーダル減衰マトリックス [c] が対角になります:
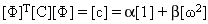(関係式 2)
Rayleigh 減衰は線形動解析スタディと非線形動解析スタディで定義できます。
Rayleigh 係数とモーダル減衰比の関係（Relation of Rayleigh Coefficients and Modal Damping Ratio）
モーダル減衰行列 [c] は次により与えられます:
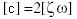(関係式 3)
i 次モードの粘性減衰係数 ci は次によって計算されます:
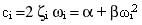(関係式 4)
および粘性減衰比 ζi は次のように表されます。
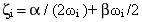(関係式 5)
i 次モードと j 次モードの減衰比が ζi と ζj の場合、Rayleigh 係数 α と β は 2 つの代数方程式の解法から計算されます:
(関係式 6)
両方のモードの減衰比が同じである場合（ζi = ζj = ζ）、α と β の値は次により与えられます。
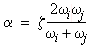（関係式 7） 
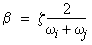（関係式 8）
他のモードの粘性減衰比 ζ は次の図にあるように振動数によって異なります:
