L'analisi armonica valuta il responso stazionario del picco di un sistema sotto carichi armonici.
Ad ogni passo di soluzione, tutti i carichi applicati ed eccitazioni base hanno la stessa frequenza. Le magnitudini sono definite dalle curve di frequenza associate.
Assumere un vettore di forza nodale armonica {P} definita come:
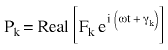 (Equazione 1) o
(Equazione 1) o 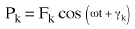 (Equazione 2),
(Equazione 2),
dove:
Pk è la magnitudine della forza nella direzione del grado di mobilità kth
ω è la frequenza di eccitazione e
Yk l'angolo fase della forza.
Per i sistemi lineari, le equazioni del sistema del movimento sono dissociate in n equazioni modali:
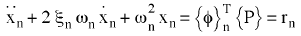 (Equazione 3).
(Equazione 3).
Sostituzione del vettore di forza {P} nei risultati (Equazione 3) in:
 (Equazione 4), dove
(Equazione 4), dove
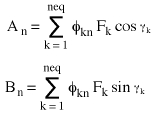 (Equazione 5)
(Equazione 5)
La soluzione dello stato stazionario (Equazione 4) è:
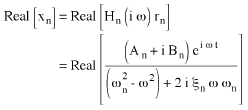 (Equazione 6).
(Equazione 6).
La parte vera di (Equazione 6) è:
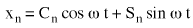 (Equazione 7), dove
(Equazione 7), dove
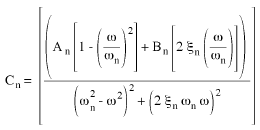 (Equazione 8) e
(Equazione 8) e
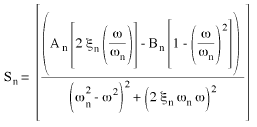 (Equazione 9).
(Equazione 9).
Il vettore di spostamento u è dato da:
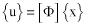 (Equazione 10) o
(Equazione 10) o
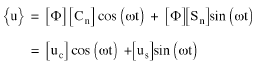 (Equazione 11)
(Equazione 11)
La magnitudine dello spostamento uk e l'angolo fase corrispondente θkper il kth grado di mobilità sono:
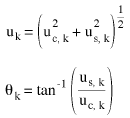 (Equazione 12)
(Equazione 12)
I responsi di velocità e accelerazione derivano dalle derivative di (Equazione 11). Le loro ampiezze sono:
 (Equazione 13)
(Equazione 13)
Gli angoli fase delle velocità e accelerazioni sono 90º e 180º sulla fase rispetto agli angoli fase dello spostamento.