Uma força adicional é aplicada quando você seleciona faces ou arestas assimétricas em relação à direção especificada da força do rolamento. Uma mensagem alerta quando a força adicional é superior a 5% da força do rolamento aplicada.
No exemplo abaixo, a entidade selecionada não é simétrica em relação à direção especificada da carga do rolamento A soma dos componentes horizontais da carga transferida P ao longo da circunferência claramente não é zero.
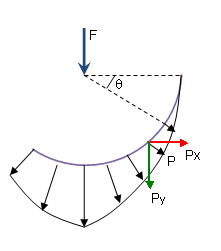
A carga adicional desequilibrada é calculada pela seguinte equação:
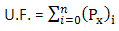
U.F. indica a força desequilibrada.
Para uma distribuição de carga senoidal:
Px = P cosΘ = Fo sinΘ cosΘ
Para uma distribuição de carga parabólica:
Px = P cosΘ = Fo sin2Θ cosΘ
A porcentagem de carga desequilibrada é calculada como (U.F./F) x 100.
Em geral, o refinamento da malha e o local do nó afetam o cálculo da força desequilibrada devido à variação de Px ao longo da circunferência.