由於人們使用鎳鈦諾的原因通常在於其承受有限應變的能力,因此對這類模型採用對數應變以及新 Lagrangian 公式。
因此,其本構模型係以對數應變與 Kirchhoff 應變零組件之關係而建立。但是,本構矩陣及應力向量兩者最終都會轉變以表示 Cauchy 應力 (真應力)。
|
σs
t1、σf
t1
|
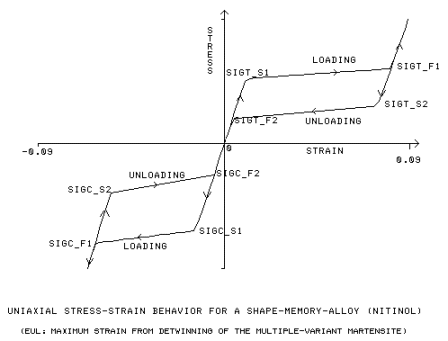
拉伸負載的初始及最終降伏強度 [SIGT_S1, SIGT_F1]
|
|
σs
t2、σf
t2
|
拉伸卸載的初始及最終降伏強度 [SIGT_S2, SIGT_F2]
|
|
σs
c1、σf
c1
|
壓縮負載的初始及最終降伏強度 [SIGC_S1, SIGC_F1]
|
|
σs
c2、σf
c2
|
壓縮卸載的初始及最終降伏強度 [SIGC_S2, SIGC_F2]
|
|
eul
|
(最大抗拉塑膠應變) *(3/2)0.5
|
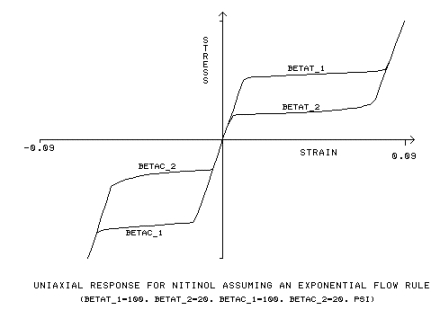
指數流動律使用額外的輸入常數 β
t1、β
t2、β
c1、β
c2:
|
βt1
|
材料參數,測量拉伸負載的轉變速率,[BETAT_1]
|
|
βt2
|
材料參數,測量拉伸卸載的轉變速率,[BETAT_2]
|
|
βc1
|
材料參數,測量壓縮負載的轉變速率,[BETAC_1]
|
|
βc2
|
bc2 = 材料參數,測量壓縮卸載的轉變速率,[BETAC_2]
|
降伏準則
為將相轉變的壓力相依之可能性模型化,故於降伏準則中採用 Drucker-Prager 型的負載函數:
F(τ) = sqrt(2)*σ(bar) + 3*α*p
F - RI
f = 0
其中
σ(bar) = 有效應力
p = 平均應力 (或靜液壓力)
α = sqrt(2/3) (σsc1 - σst1 ) / (σsc1 + σst1)
Rf
I = [ σf
I(sqrt(2/3) + α)],I = 1 適用於負載,而 2 適用於卸載