Analizę harmoniczną należy wykorzystywać do obliczania szczytowej reakcji w stanie ustalonym spowodowanej obciążeniami harmonicznymi lub wzbudzeniami podstawowymi.
Obciążenie harmoniczne P jest wyrażane w postaci P = A sin (ωt + φ), gdzie: A oznacza amplitudę, ω oznacza częstotliwość, t oznacza czas, a φ oznacza kąt fazowy. Poniżej pokazano przykładowe obciążenia harmoniczne o różnych częstotliwościach w względem czasu:
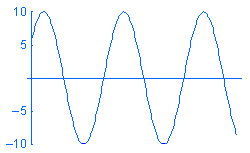
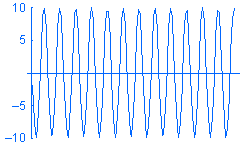
Pomimo że możliwe jest tworzenie badania historii modalnej i definiowanie obciążeń w funkcji czasu, przejściowa zmienność reakcji w czasie może nie być dla nas interesująca. W takich przypadkach można zaoszczędzić czas i zasoby poprzez rozwiązanie dla szczytowej reakcji w stanie ustalonym przy żądanym zakresie częstotliwości roboczej przy użyciu analizy harmonicznej.
Na przykład napęd zainstalowany na stanowisku badawczym przenosi obciążenia harmoniczne na układ wsporczy za pośrednictwem śrub. Można wymodelować układ wsporczy i zdefiniować badanie harmoniczne, aby oszacować szczytowe przemieszczenia, naprężenia itp. w stanie ustalonym dla zakresu częstotliwości roboczych napędu. Napęd można przybliżyć jako rozprowadzoną masę.
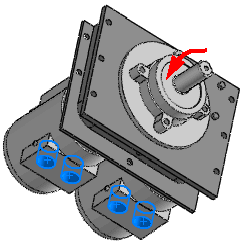
Po uruchomieniu badania można wyświetlić szczytowe amplitudy parametrów reakcji (naprężenia, przemieszczenia, przyspieszenia i prędkości), jak również grafy reakcji kątów fazowych parametrów reakcji w zakresie częstotliwości roboczych.
W przypadku uruchomienia badania harmonicznego wykres konturowy parametru reakcji pokazuje bezwzględne wartości szczytowe historii sinusoidalnej czasu reakcji w danym kroku częstotliwości. Przejściowa sinusoidalna część parametru reakcji i jej kąt fazowy nie są pokazane na wykresie. W przypadku kroku częstotliwości roboczej bliskiego naturalnej częstotliwości modelu wykres postaci drgań jest bardziej rzeczywistą reprezentacją zdeformowanego kształtu niż wykres konturów przemieszczenia w danej częstotliwości.
Można utworzyć graf reakcji kąta fazowego dla parametru reakcji (naprężenia, przemieszczenia, przyspieszenia czy prędkości) w zakresie wszystkich kroków częstotliwości rozwiązania.
Dla analizy tego typu są dostępne opcje tłumienia modalnego, Rayleigha i modalnego złożonego.