Estudos dinâmicos não lineares

Para a análise dinâmica não linear, é seguido o mesmo procedimento usado para a análise estática não linear: Controle, Iteração e Terminação.

Na análise dinâmica não linear, as equações de equilíbrio do sistema dinâmico na etapa de tempo, t+Δt, são:

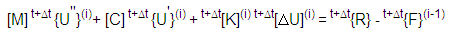
onde:

[M] = Matriz de massa do sistema

[C] = Matriz de amortecimento do sistema

^t+Δt[K]⁽ⁱ⁾ = matriz de rigidez do sistema

^t+Δt{R} = Vetor de cargas de nó aplicada externamente

^t+Δt{F}^(i-1) = Vetor das forças dos nós geradas internamente da iteração (i-1)

^t+Δt[ΔU]⁽ⁱ⁾ = Vetor dos incrementos de deslocamento de nós da iteração (i)

^t+Δt{U}⁽ⁱ⁾ = Vetor dos incrementos de deslocamento de nós da iteração (i)

^t+Δt {U^'}⁽ⁱ⁾ = Vetor dos incrementos de deslocamento de nós da iteração (i)

[M] ^t+Δt {U^''}⁽ⁱ⁾ = Vetor dos deslocamentos totais na iteração (i)

Usando esquemas de integração de tempo implícito como os métodos Newmark-Beta ou Wilson-Theta, e empregando um método iterativo de Newton, as equações acima são reunidas no formato:

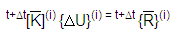
onde:

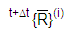= vetor de carga efetivo

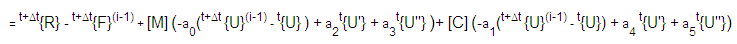
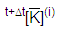= a matriz de rigidez efetiva =^t+Δt[K]⁽ⁱ⁾ + a₀[M] + a₁[C]