并非所有应力热点都与应力奇异性相关联。 在热点区域局部细化网格可以消除归因于非奇异的应力集中的这些应力热点。
应力奇异性的特性行为是应力值和网格细化(局部使用网格控制或通过全局编辑网格)一起保持增长,理论上正发散到无限。 如果应力热点元素处的应力不随网格细化增长并朝有限值收敛,那么表明它们应力集中(“合理”的高应力区域)。
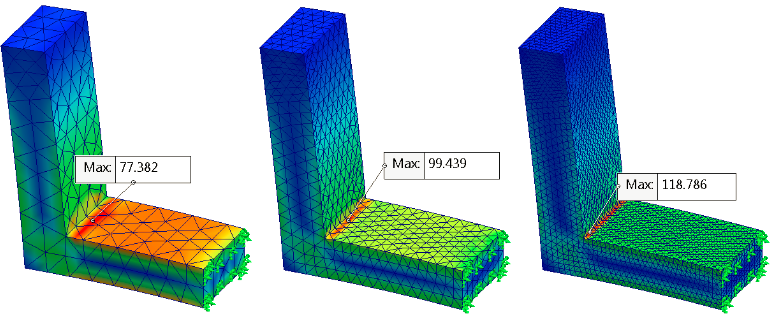 |
| 在锐凹角附近发散应力,因为得到细化的网格表明了应力奇异性。 |
应力集中的特点是模型局部区域中相邻元素的相对大应力梯度。 既然网格已足够细化,归因于合理应力集中的高应力梯度将收敛为有限值。 它们在几何体中有变化的位置为可见,比如板中孔的存在之处、不同材料存在的边界处和实体进行接触的点位置。
 |
| 在孔附近收敛应力,因为网格细化表明应力集中。 |
您可以在文献资料中为有问题的最大应力/标称应力的应力集中系数找到分析解决方案的广义数据(Young, W., Budynas, R., (2001),Roark 的《应力和应变的公式》(Formulas for Stress and Strain)第 17 章– 弹性应力的应力集中系数 (Kt))
视为应力奇异性的建议
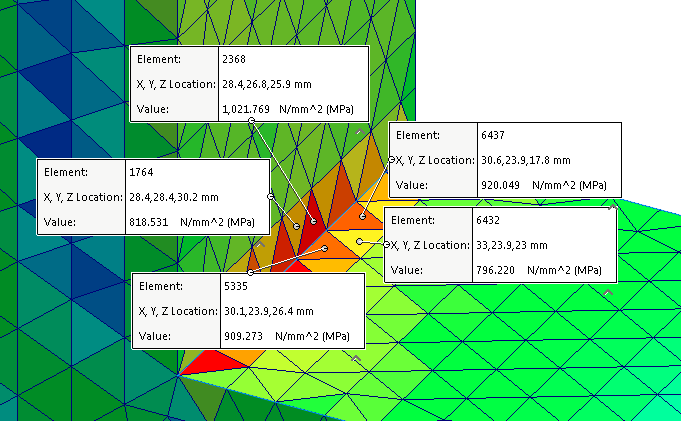
- 要区分合理应力集中的应力奇异性,需全局细化网格或在检测应力热点的局部区域进行细化。 当您重新运行应力热点诊断工具时,应过滤应力集中的区域,剩余的应力热点会指出应力奇异性。 请注意,在物理世界中不会发生应力奇异性,因为当应力超出材料的终极强度限制时,材料将屈服或断裂。
- 将圆角添加到锐边和发生高应力梯度的“圆形”角位置。 圆角在更广泛的区域内分布应力并有效地增加了零件的载荷轴承能力。 记住,现实世界中制造的“尖角”将始终有小的圆角半径。
 |
| 锐边处的不规则应力分布。 |
 |
| 圆角处的平滑应力分布。 |
- 如果可以的话,避免在顶点上或沿边线应用载荷。 将载荷分布到模型上适合的从属区域以近似于尽可能准确的实际载荷条件。 记住,即使将载荷用作创建应力奇异性的奇异点载荷 (σ = P/A and A=0 → σ=∞),应力分布远离应用载荷的某些距离仍然正确无误。 此载荷基于 St。 声明了两个不同效果但静态对等的载荷之间的 Venant 原理在足够大的载荷距离处变得非常小。
- 应力奇异性仅可以局部影响应力分布。 您可能会忽略这些应力奇异性的局部区域,尤其是如果它们不在模拟中相关区域附近时,则请检查应该保持“未受影响”的更远的应力结果。