Damping Effects
If you apply initial conditions to a dynamic system, the system vibrates
with decreasing amplitudes until it comes to rest. This phenomenon is
called damping. Damping is a complex phenomenon that dissipates energy
by many mechanisms like internal and external friction, thermal effects
of cyclic elastic straining materials at the microscopic level, and air
resistance.
It is difficult to describe dissipation mechanisms mathematically. Damping
effects are usually represented by idealized mathematical formulations.
For many cases, damping effects are adequately described by equivalent
viscous dampers.
A viscous damper (or dashpot)
generates a force that is proportional to velocity. A piston that can
move freely inside a cylinder filled with a viscous fluid like oil is
an example of a viscous damper. The damping force Fd is
assumed to be linear with respect to the relative velocity at the two
ends of the damper:
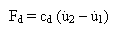(Equation 1).
The constant cd, which is
the slope of the curve Fd
versus the relative velocity is called the coefficient
of viscous damping;
The units of coefficient of viscous damping are (force)/(velocity) or
(force x time)/(length).
The response of a general viscously damped n-degree-of-freedom
system is given by:
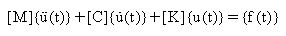(Equation
2), where:
[M] = n
x n symmetric
mass (or inertia) matrix
[C] = n
x n symmetric
damping matrix
[K] = n
x n symmetric
stiffness matrix
{f(t)} =
n-dimensional
force vector
, 
, 
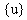are the displacement, velocity,
and acceleration n-dimensional
vectors, respectively.
In general, classical modal analysis
does not necessarily lead to an independent system of equations of motion
unless the damping matrix [c]
resulting from the modal coordinate transformation can be treated as a
diagonal matrix.
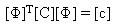(Equation 3)
The following types of damping are available:
Related Topics
Modal
Time History Analysis
Harmonic
Analysis
Random
Vibration Analysis