Modelo hiperelástico de Mooney - Rivlin
A função de densidade de energia de deformação de Mooney-Rivlin é expressa como:

onde I, II e III são constantes do tensor à direita de distorção Cauchy-Green Cauchy-Green e pode ser expresso em termos das razões de alongamento principais; A, B, C, D, E e F são constantes de Mooney do material, e
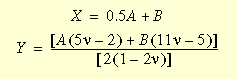
Deve ser notado que quando o material se aproxima da incompressibilidade, a terceira constante, III, se aproxima da unidade, ao passo que Y tende ao infinito. Assim, para valores do coeficiente de Poisson próximos a 0,5, o último termo em w
1 permanece restrito, podendo-se, então, obter uma solução.
O modelo de material de Mooney-Rivlin pode ser usado com elementos sólidos e cascas espessas. As propriedades de material para o modelo de Mooney-Rivlin são dados de entrada para a caixa de diálogo Material. bsp;Até seis constantes Mooney-Rivlin podem ser inseridas: Mooney_A, Mooney_B, Mooney_C, Mooney_D, Mooney_E, and Mooney_F.
As constantes do modelo Mooney-Rivin são calculadas automaticamente quando a opção Usar dados da curva para calcular constantes do material na caixa de diálogo
Material
está marcada. As constantes são salvas em um arquivo de texto com a extensão .log na pasta de resultados ativa para o estudo.
NOTAS
-
Usar o método iterativo de NR (Newton-Raphson).
-
São aceitáveis valores de coeficiente de Poisson maiores ou iguais a 0,48, mas menores do que 0,5. Quando a fórmula deslocamento-pressão é utilizada, o coeficiente de Poisson recomendado fica no intervalo entre 0,499 e 0,4999.
-
Os materiais semelhantes a borracha geralmente deformam-se rapidamente sob carregamentos de menor magnitude, exigem portanto que o carregamento inicial seja mais lento.
-
Ao lidar com materiais semelhantes à borracha, poderá ocorrer, devido ao comportamento altamente não linear do problema, um aumento rápido no carregamento, muitas vezes resultando em instabilidade numérica (termos diagonais negativos na rigidez) ou, então, em divergência durante iterações de equilíbrio. O algoritmo adaptativo automático de divisão em etapas pode ajudar nesses casos.
-
O deslocamento ou o controle de comprimento do arco podem se demonstrar mais eficazes do que o controle de força quando termos diagonais negativos ocorrem repetidamente sob várias taxas de carregamento.
-
Para os elementos de casca com fórmula grossa, a análise é simplificada, pois a incompressibilidade não resulta em termos irrestritos. A fórmula é derivada com a pressuposição de perfeita incompressibilidade (coeficiente de Poisson de 0,5) e, portanto, o NUXY é desprezado.
-
As constantes A e B devem ser definidas de modo que (A+B) > 0. Para mais informações sobre como determinar os valores das constantes A and B, consulte o trabalho de .
Para definir modelos hiperelásticos...