Modello di plasticità von Mises

Il criterio di snervamento può essere scritto come:

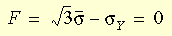
dove s è la sollecitazione effettiva e s Y è la sollecitazione di snervamento riportata nei test uniassiali. Il modello von Mises può essere utilizzato per descrivere il comportamento dei metalli. Quando viene utilizzato questo modello, è importante considerare quanto segue:

• Si presuppone una lieve plasticità da sollecitazione quando viene utilizzato uno spostamento piccolo o grande.

• Si presuppone una regola di flusso associata.

• Sono disponibili le regole di indurimento isotropo e cinematico. Un abbinamento lineare dell'indurimento isotropico e cinematico viene implementato quando sia il raggio che il centro della superficie nello spazio deviatorico possono variare rispetto alla cronologia del caricamento.

Il parametro RK definisce la proporzione dell'indurimento cinematico e isotropico.

Per l'indurimento puro isotropico, il parametro RK ha il valore 0. Il raggio della superficie si espande ma il suo centro rimane fisso nello spazio deviatorico.

Per l'indurimento puro cinematico, il parametro RK ha il valore 1. Il raggio della superficie rimane costante mentre il suo centro può spostarsi nello spazio deviatorico.

• Per la plasticità è possibile immettere una curva di sollecitazione-deformazione uniassiale di tipo bilineare o multilineare. Per la definizione di una curva di sollecitazione-deformazione bilineare, lo snervamento e il modulo elastico vengono immesse attraverso la finestra Materiale. Per la definizione di una curva di sollecitazione-deformazione multilineare, è necessario definire una curva di sollecitazione-deformazione.

• Quando viene definita una curva di sollecitazione-deformazione, il primo punto sulla curva deve essere il punto di snervamento del materiale. Le proprietà del materiale, quali modulo elastico, snervamento, etc. saranno richiamate dalla curva di sollecitazione-deformazione, quando disponibile, e non dalla tabella delle proprietà del materiale nella finestra di dialogo Materiale. Solo il coefficiente di Poisson (NUXY) sarà richiamato dalla tabella.

La definizione delle curve di sollecitazione-deformazione non è supportata negli studi del test di caduta.

• I parametri di snervamento e modulo elastico per la descrizione della curva di sollecitazione-deformazione possono essere associati alle curve della temperatura per l'esecuzione dell'analisi termoplastica.

• Si consiglia l'uso del modello iterativo NR (Newton-Raphson).

Il modello Huber-von Mises può essere usato con gli elementi solidi (qualità bozza e alta) e di shell spesso (qualità bozza e alta).

La termoplasticità non è disponibile con gli elementi shell.

Nella seguente figura viene illustrata una tipica curva di sollecitazione-deformazione di un materiale plastico:

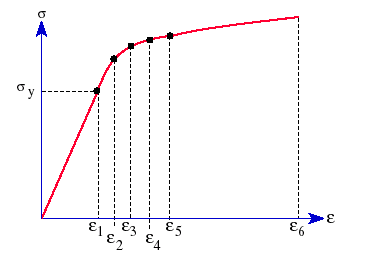
Analisi di forte deformazione

Nella teoria della plasticità con forte deformazione, viene definito il valore della deformazione logaritmica come:

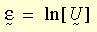
dove U è il tensore di stiramento destro solitamente ottenuto dalla scomposizione del polo destro del gradiente di deformazione F (ad esempio, F = R U, R è il tensore di rotazione). La deformazione logaritmica incrementale è calcolata come:

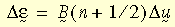
dove B (n+1/2) è la matrice di deformazione-spostamento stimata al passo di soluzione n+1/2 e D u è il vettore degli spostamenti incrementali. Si osservi che la formula sopra riportata è un'approssimazione di secondo ordine della formula esatta.

Il coefficiente di sollecitazione è preso dal coefficiente Green-Naghdi per garantire la correttezza del modello costitutivo. Trasformando il coefficiente di sollecitazione dal sistema globale al sistema R,

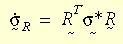
L'intero modello costitutivo avrà la stessa forma della teoria della lieve deformazione. La teoria della plasticità da forte deformazione viene applicata al criterio di snervamento von Mises, alla regola di flusso associativo e all'indurimento cinematico e isotropo (bilineare o multilineare). La dipendenza dalla temperatura della proprietà del materiale è supportata dall'indurimento bilineare. Nel presente caso, viene usato l'algoritmo di ritorno radiale. L'idea di base è approssimare il vettore normale N con:

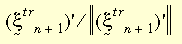
dove:

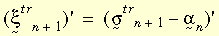
Nella seguente figura vengono illustrate le due precedenti equazioni.

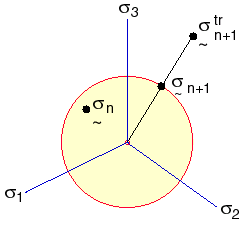
Il vettore di forza dell'elemento e le matrici di rigidezza sono calcolati in base alla formula di Lagrange aggiornata. Le sollecitazioni di Cauchy, le deformazioni logaritmiche e lo spessore attuale (solo elementi shell) sono salvati nel file di output.

L'elasticità nel presente caso è modellata in forma iperelastica, presupponendo piccole deformazioni elastiche e consentendo arbitrariamente forti deformazioni plastiche. Per i problemi di elasticità di forte deformazione (materiali gommosi), è possibile utilizzare modelli di materiali iperelastici, come ad esempio Mooney-Rivlin.

La sollecitazione Cauchy (vera) e la deformazione logaritmica devono essere utilizzate nella definizione della curva di sollecitazione-deformazione multilineare.

Confronto fra i criteri per la plasticità Tresca e von Mises