针对在给定工作频率或随机振动环境下承受反复周期性载荷的零件,您可以预测其损坏程度和剩余寿命。
可用于 SOLIDWORKS Simulation Premium。
您可以基于频域事件执行疲劳分析,其中的事件使用线性动态谐波和线性动态随机振动算例的结果。
基于频域事件的疲劳算例输出包括剩余寿命和损坏图解。 针对基于随机振动的疲劳算例,输出还包括失效时间图解。
基于谐波结果的疲劳
基于线性动态谐波算例的应力结果(作为频率功能)的疲劳算例可预测零件的剩余寿命和损坏程度,其中零件在一定工作频率下承受反复的周期(或正弦)振动。
累积损坏率的计算基于线性损伤法则或密纳法则:
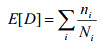
其中 E [D] 代表预期损坏率;nI 代表零件在一定工作频率和交替应力 SI 环境下的周期数;NI 代表在由材料 S-N 曲线决定的应力等级 SI 下足以导致失败的周期数。
基于随机振动结果的疲劳
如果结构或零部件的历史记录显示其应力和应变具有随机特性(因此可使用概率密度功能、向上零交叉和每秒峰值数等参数完美描述),要预测疲劳寿命,您可以使用以下频域计算方法:
基于频率的疲劳寿命预测假定被分析的模型响应参数(应力和应变)具有随机、恒定和高斯特性。
不同于其他疲劳算例,材料 S-N 曲线使用 Basquin 方程式来定义:
N = B / (Se )m
其中 N = 容许的失败周期数;B = 特定于曲线的常数(S 轴的截距);Se = 周期性载荷的应力范围;m = 线性 S-N 曲线的斜率。
该方程式表明在恒定振幅周期性载荷条件下,当图解使用重对数图尺时,失败周期数 N 与应用的应力范围 Se 之间存在线性关系。