Os seguintes métodos de integração são usados em estudos de vibração aleatória:
Método padrão
O método padrão para análise de vibração aleatória é realizado da seguinte maneira:
-
Determinados pontos de frequência são selecionados em torno de cada modo natural solicitado. A localização desses pontos depende do valor do parâmetro de tendência p.
O parâmetro de tendência 1,0 indica que todos os pontos de frequência estão uniformemente distribuídos entre as frequências naturais. Se o parâmetro de tendência for maior do que 1,0, os pontos estão selecionados mais próximos das frequências naturais. The default values for the frequency points and the biasing parameter are given as a function of the first mode's damping ratio ζ. For an illustration on the selection of the frequency points click here.
Os valores predeterminados dos pontos de frequência e do parâmetro de tendência como uma função de z são mostrados a seguir:
| Razão de amortecimento modal
|
Número de frequências (predeterminado)
|
Parâmetros de tendência (predeterminado)
|
|---|
| ζ < 0.01
|
21 |
11
|
| 0,01 < ζ < 0,1 |
21-4.34 ln(z /0,01)
|
11-3.47 ln(z /0,01)
|
| ζ > 0.1
|
11
|
3
|
The software applies the default values given in Table 1 when zero (0) is defined for both the Number of frequency points and Biasing Parameter.
- PSDs modais de resposta são avaliadas em cada ponto de frequência. A razão de corte do modo cruzado (TAXA) define um limite na taxa de todos os pares de frequências naturais possíveis (wi / wj, i > j).
Isso significa que, para cada par de modos comwi / wj > TAXA, os termos de densidade de espectro cruzado são desprezados. Os efeitos de modo cruzado não são considerados para TAXA = 1.
- As psds modais são então integradas numericamente no intervalo de frequência especificado para fornecer os valores médios quadráticos e as covariâncias da resposta modal. A integração é efetuada numericamente utilizando a integração de Gauss de ordem 2 ou 3 em cada intervalo de frequência, com base em uma interpolação log-log. A resposta média quadrática é obtida somando as contribuições do intervalo.
- Finalmente, a transformação de modal para nodal fornece deslocamentos, acelerações e velocidades rms do sistema.
Método aproximado
O método padrão de integração pode ser demorado devido à integração numérica de grandes matrizes. O método aproximado de integração obtém uma solução simplificada ao estabelecer as seguintes suposições:
- Desprezar a resposta de modo cruzado, Sx(ω), que é o efeito de um modo sobre o outro, ou seja,
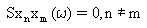(Equação 1)
- As psds de excitações são consideradas constantes em torno de cada modo. Assim, pressupõe-se que cada modo seja excitado por "ruído branco" com densidade espectral Sn, onde;
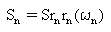(Equação 2)
ωn é a frequência natural do modo n (n = 1,2,...nf).
Para o ruído branco, as respostas médias quadráticas podem ser determinadas analiticamente para as respostas modais:
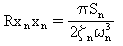(Equação 3)
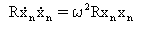(Equação 4)
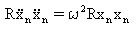(Equação 5).