Use a análise harmônica para calcular a resposta de pico em estado estável devido a cargas harmônicas ou excitações de base.
A harmonic load P is expressed as P = A sin (ωt + φ) where: A é amplitude, w é frequência, t é tempo e f, o ângulo da fase. Apresentamos a seguir uma amostra de cargas harmônicas de diferentes frequências w em função do tempo:


Embora seja possível criar estudos de histórico de tempo modal e definir as cargas como funções do tempo, você talvez não esteja interessado na variação transiente da resposta em relação ao tempo. Nesses casos, você poupa tempo e recursos usando a análise harmônica para obter a solução para a resposta de pico em estado estável no intervalo de frequência operacional desejado.
Um motor montado em uma bancada de teste, por exemplo, transfere cargas harmônicas para o sistema de suporte através dos parafusos. Você pode modelar o sistema de suporte e definir um estudo harmônico para avaliar picos de deslocamento em estado estável, tensões, etc., para o intervalo de frequências operacionais do motor. Você pode aproximar o motor por uma massa distribuída.
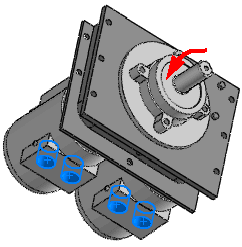
Após a execução do estudo, você pode ver os picos de tensão, deslocamentos, acelerações, velocidades e ângulos de fase da resposta ao longo do intervalo de frequências operacionais.
As opções de amortecimento modal, Rayleigh e modal composto estão disponíveis para este tipo de análise.