O sistema de equações de movimento para um sistema linear com n graus de liberdade, excitado por uma força que varia com o tempo, é:
(Equação 1)
onde:
[M] = matriz simétrica n x n da inércia
[C] = matriz simétrica n x n do amortecimento
[K] = matriz simétrica n x n da rigidez
{f(t)} = vetor de força n-dimensional
{u}, 
e 
são os vetores n-dimensionais de deslocamento, velocidade e aceleração, respectivamente.
A (Equação 1) é um sistema de n equações diferenciais ordinárias simultâneas com coeficientes constantes. As equações de movimento são combinadas através dos termos de massa, rigidez e amortecimento. A combinação depende do sistema de coordenadas utilizado para descrever matematicamente as equações de movimento.
A ideia básica da análise modal é transformar o sistema combinado da (Equação 1) em um conjunto de equações independentes usando a matriz modal [Φ] como matriz de transformação. [Φ]contém os modos normais {f}i for i = 1, ....,n, ...., n organizado como:
(Equação 2)
Os modos normais e autovalores (eigenvalues) do sistema são derivados da solução do problema de autovalor:
(Equação 3)
onde [ω2] é a matriz diagonal do quadrado das frequências naturais.
Em sistemas lineares, o sistema de n equações de movimento pode ser separado em n equações com um único grau de liberdade em termos do vetor de deslocamento modal {x}:
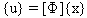(Equação 4)
Substituindo o vetor {u} na (Eq.4) e pré-multiplicando-o por [Φ]T (Equação 1), obteremos:
(Equação 5)
Os modos normais satisfazem a propriedade de ortogonalidade e a matriz modal [Φ] é normalizada para satisfazer as seguintes equações:
(Equação 6)
(Equação 7) e
(Equação 8).
Substituindo as (Equações 6--8), a (Equação 5) se torna um sistema de n equações diferenciais SDOF independentes de segunda ordem:
para i = 1, ..., n (Equação 9)
A (Equação 9) é resolvida utilizando métodos de integração passo a passo, como Wilson-Teta e Newmark.
A integração é realizada no domínio do tempo, onde os resultados da última etapa são usados para prever os resultados da etapa seguinte.
O vetor de deslocamento (u) do sistema é derivado da (Equação 4).