Model tečení

Tečení je časově závislé namáhání vzniklé za stavu konstantního napětí.

Tečení bylo pozorováno ve většině materiálů, zvláště kovech za vyšší teploty, plastech vyšších polymerů, betonu a pevných palivech v raketových motorech. Vzhledem k tomu, že vznik tečení trvá dlouho, v dynamické analýze se jeho vlivy většinou zanedbávají.

Křivka tečení je graf namáhání v čase. V křivce tečení je možné rozpoznat tři různé režimy; první, druhý a třetí. Zájem je většinou a primární a sekundární režimy.

fig_6.gif

Je implementován klasický zákon síly pro tečení (zákon Bailey-Norton) založený na rovnici stavu. Tento zákon definuje výraz pro jednoosé namáhání tečení za podmínek jednoosého napětí a času.

Klasický zákon síly pro tečení (zákon Bailey-Norton)

a

kde:

T = teplota prvku (v kelvinech)

CT = Konstanta materiálu určující závislost tečení na teplotě

C0 je Konstanta tečení 1, která se zadává na záložce Vlastnosti v dialogovém okně Materiál.

Konstanta tečení 1 musí mít zadané jednotky v systému SI. Koeficient převodu se rovná 1/ (napětí ^ (C1) * čas ^ (C2)). Jednotky napětí jsou v N/m2 a čas je v sekundách.

C1 je Konstanta tečení 2 a C2 je Konstanta tečení 3 v dialogovém okně s vlastnostmi materiálů.

Klasický zákon síly pro tečení představuje primární a sekundární režimy tečení v jednom vzorci. Terciární režim tečení se neuvažuje. „t“ je aktuální skutečný (ne pseudo) čas a sigma je celkové jednoosé napětí v čase t.

Aby tyto zákony platily pro chování víceosého tečení, vychází se z následujících předpokladů:
  • Zákon jednoosého tečení zůstává platný v případě, že jednoosé namáhání tečením a jednoosé napětí jsou nahrazeny svými efektivními hodnotami.
  • Materiál je izotropní
  • Namáhání při tečení jsou nestlačitelná

U numerické analýzy tečení, kde může být použito cyklické zatěžování, jsou podle pravidla tvrzení poměry aktuálního namáhání tečením vyjádřeny funkce aktuálního napětí a celkového namáhání tečením:

: účinné napětí v čase t
:celkové účinné namáhání tečením v čase t
: součásti výchylkového tenzoru napětí v čase t

Odvození konstant tečení z referenčních dat

V tomto příkladu odvodíte konstanty tečení z referenčních dat pro materiál Nerezová ocel.

Podle klasického mocninného zákona tečení (Bailey - Nortonův zákon) je napětí na mezi tečení v čase t, zatímco se ignoruje kolísání teploty, dáno následujícími vztahy:



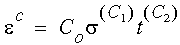
V dialogu Materiál konstanty C0, C1 a C2 označují následující:

C0 = Konstanta tečení 1, C1 = Konstanta tečení 2 a C2 = Konstanta tečení 3

Ve výše uvedené rovnici: se Konstanta tečení 1 ( C0) vypočítá v systému jednotek SI (napětí je N/m 2 a čas v sekundách), Konstanta tečení 2 ( C1 >1) je bez jednotek a Konstanta tečení 3 (C2) je v rozsahu 0 až 1.

Z referenčních dat tečení níže se vypočítají konstanty tečení pro rovnici stavu tečení. Tabulka odkazuje na hodnoty konstantního napětí při konstantních teplotách, při kterých se může po delší době vyvinout 1% napětí na mezi tečení. Tato data odkazují na Nerezovou ocel - třída 310.
Teplota (° C) Napětí (MPa) Napětí (MPa)
Čas = 10 000 h Čas = 100 000 h
550 110 90
600 90 75
650 70 50
700 40 30
750 30 20
800 15 10
Vyberte data napětí pro teplotu 550 C. Pokud uvažujeme C2 =1 z výše uvedené rovnice stavu tečení, získáme systém 2 rovnic se 2 neznámými C0 a C1. Nejprve vypočítáme C1. Dvě rovnice stavu tečení pak jsou:

0,01 = C0 * 110 C1* 10 000 (rovnice1)

0,01 = C0 * 90 C1* 100 000 (rovnice 2)

Porovnání dvou rovnic a použití logaritmických funkcí:

C1 * log (110) = C1 * log (90) +1 (rovnice 3)

Z rovnice 3 vypočítáme C1 = 11.47.

Můžeme použít rovnici 1 nebo rovnici 2 k vypočítání C0. C0 se vypočítá v jednotkách SI (může být potřeba použít přepočítávací faktory).

C0 = 0.01 / ( (90E6)11.47 * 100000 *3600) = 1.616E-102

Zadejte tři konstanty tečení do dialogu Materiál:

Konstanta tečení 1 = 1.616E-102 , Konstanta tečení 2 = 11.47, Konstanta tečení 3 = 1

V dialogu Materiál vyberte Použít účinky tečení pro aktivování výpočtu tečení pro vybraný model materiálu. Výpočty tečení se dělají pouze pro nelineární studie. Efekt tečení není dostupný pro lineární elastické ortotropní a viskózně elastické modely materiálu.

Nastavení řešiče pro výpočet tečení

  • V dialogu Materiál vyberte Použít účinky tečení pro aktivování výpočtu tečení pro vybraný model materiálu. Výpočty tečení jsou podporovány pouze pro nelineární studie s objemovou sítí. Účinky tečení nejsou podporovány pro skořepiny nebo nosníky. Zohlednění tečení není dostupné pro lineární elastické ortotropní a viskózně elastické modely materiálu.
  • Při zvažování efektu tečení v nelineární studii vyberte možnost Automaticky (automatické odstupňování) pro zvýšení pravděpodobnosti konvergence (dialog Nelineární studie). Řešič vypočítá původní hodnotu pro napětí na mezi tečení εorg a pokud εorg překročí 1.0, řešení se ukončí. Pokud řešič překročí maximální počet iterací rovnováhy potřebných pro dosažení konvergence, řešení se ukončí a řešič zobrazí odpovídající chybové zprávy s akcemi pro nápravu.
  • Pro možnost Řešič vyberte Automatický výběr řešiče.
  • Zadejte Čas ukončení v sekundách (dialog Nelineární studie).