V teorii plasticity velkého namáhání je logaritmické měření namáhání měřeno takto: 
, kde U je pravý tenzor natažení obvykle získaný z pravého polárního rozložení gradientu deformace F (tedy F = R U, R je tenzor rotace). Přírůstkové logaritmické namáhání se odhadne jako: 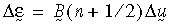
, kde B(n+1/2) je matice namáhání-posunutí odhadnutá v kroku řešení n+1/2 a Δu je vektor přírůstkových posunutí. Tato forma je aproximace druhého řádu přesného vzorce.
Poměr napětí se získá jako poměr Green-Naghdi, aby byl základní model rámcově neměnný a objektivní. Transformací poměru napětí z globálního systému na R-systém získáme tento vztah:
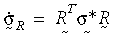
Celý základní model bude mít stejnou formu pro teorii malého namáhání. Teorie plasticity velkého namáhání se použije pro kritérium tažnosti von Mises, asociativní pravidlo proudu a izotropní nebo kinematické tvrzení (bilineární nebo vícelineární). Závislost na teplotě vlastnosti materiálu je podporována bilineárním tvrzením. V aktuálním případě se použije algoritmus radial-return (radiálního návratu). Základní myšlenkou je aproximace normálového vektoru N:
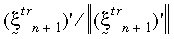
kde 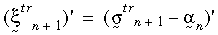
Následující obrázek ilustruje dvě předchozí rovnice.
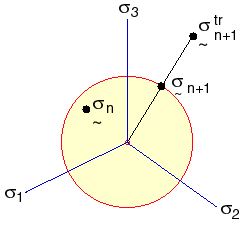
Vektor síly prvku a matice tuhosti se vypočítají podle aktualizované Lagrangeovy formulace. Do výstupního souboru se zaznamenají Cauchyho napětí, logaritmická namáhání a aktuální tloušťky (pouze prvky skořepiny).
Pružnost se v aktuálním případě modeluje v hyperelastické formě, která předpokládá malá elastická namáhání, ale počítá s libovolně velkým plastickým namáháním. U problémů s velkým elastickým namáháním (gumové materiály) lze použít hyperelastické modely materiálů, například Mooney-Rivlinův.
Při definování vícelineární křivky závislosti mezi napětím a namáháním použijte Cauchyho (skutečné) napětí a logaritmické namáhání.