Kritérium tažnosti lze zapsat touto formou: 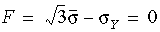
, kde
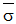
je efektivní napětí a σ
Y je mez kluzu z jednoosých testů. Pomocí modelu von Mises lze popsat chování kovů. Při používání tohoto modelu materiálu nezapomeňte na následující okolnosti:
- Při použití velkého nebo malého posunutí se předpokládá plasticita malého namáhání.
- Provede se předpoklad přidruženého pravidla proudu.
- K dispozici jsou pravidla izotropního i kinematického tvrzení. Lineární kombinace izotropního a kinematického tvrzení se použije v případě, že se poloměr a střed povrchu deformace v prostoru odchylek může vzhledem k vývoji zatížení lišit.
Parametr RK definuje poměr kinematického a izotropního tvrzení. U zcela izotropního tvrzení má parametr RK hodnotu 0. Poloměr povrchu deformace se zvětší, ale střed zůstává v prostoru na stejném místě. U zcela kinematického tvrzení má parametr RK hodnotu 1. Poloměr povrchu deformace zůstává stejný, zatímco střed se v prostoru může pohybovat.
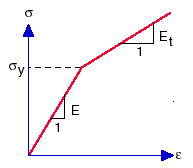
Zadat lze bilineární nebo vícelineární jednoosou křivku závislosti mezi napětím a namáháním pro plasticitu. Pro definici bilineární křivky závislosti mezi napětím a namáháním se mez kluzu, modul pružnosti a modul tečny zadávají v dialogovém okně Materiál. Pro definici vícelineární křivky závislosti mezi napětím a namáháním je nutné definovat křivku závislosti mezi napětím a namáháním.
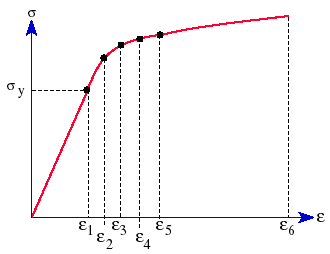
Když definujete křivku závislosti mezi napětím a namáháním, měl by první její bod být bodem deformace materiálu. Vlastnosti materiálu, například modul pružnosti, mez kluzu a další, se nezískávají z tabulky vlastností materiálů v dialogovém okně Materiál, ale z dostupné křivky závislosti mezi napětím a namáháním. Z tabulky se získá pouze Poissonova konstanta (NUXY).
Studie pádových zkoušek mohou používat pouze bilineární křivky závislosti mezi napětím a namáháním pro tvárnost. Pokud definujete vícelineární křivku závislosti mezi napětím a namáháním a spustíte studii pádových zkoušek, bude ji řešič ignorovat.
Parametry mez kluzu a modulu pružnosti pro popis bilineární křivky závislosti mezi napětím a namáháním lze přidružit ke křivkám teplot a provést termoplastickou analýzu. Teplotní plasticita není u elementů skořepiny k dispozici.
Model Huber-von Mises lze použít u objemových elementů a elementů s širokou skořepinou (v nízké i vysoké kvalitě).
Doporučuje se použít iterační metodu NR (Newton-Raphson).
Typická křivka závislosti mezi napětím a namáháním plastového materiálu: