對隨機振動環境中運作的零組件而言,其疲勞損害評估會根據回應應力功率頻譜密度 (PSD) 函數的統計資料屬性在頻率網域中估計。
當結構或機械零組件承受隨機負載形式 (例如風負載下的風渦輪、波浪負載下的離岸結構或在不同道路曲面輪廓上的汽車引擎作業) 時,疲勞壽命估計值會在頻率網域中進行估計。
振動疲勞 (或頻率式疲勞) 一詞代表的是疲勞壽命估計值,其中的負載和回應 (應力與應變的歷程) 是隨機程序,因此最適合使用如功率頻譜密度 (PSD 函數) 等統計測量進行描述。
您可以透過 PSD 函數的力矩取得回應應力 PSD 的統計資料特性。
| PSD 的統計資料特性 |
數學方程式 |
|---|
| 應力 PSD S(f) 在頻率 f (以 Hz 為單位) 的第 n次頻譜力矩。 |
 (方程式 1) (方程式 1)
|
| 連續不動之高斯程序 σ 的均方根值。 |
 (方程式 2) (方程式 2)
|
| 一般 1 秒範例向上零交錯 E[0] 的平均數目。 |
 (方程式 3) (方程式 3)
|
| 一般 1 秒範例峰值 E[p] 的平均數目。 |
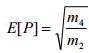 (方程式 4) (方程式 4)
|
| 不規則性係數 γ 會介於 0 和 1 之間。在應力訊號接近窄頻程序 (對於正弦波 γ =1) 時,它會接近 1。 在應力訊號接近白色雜訊程序時,它會接近 0。 |
 (方程式 5) (方程式 5)
或
 (方程式 6) (方程式 6)
|
材質疲勞屬性通常是從 S-N 曲線取得,該曲線定義了應力範圍之間的關係,即 S (這是從張力最大循環應力到壓縮最小循環應力的應力變化) 相對於平均失敗週期數 N 的關係。
大部分的高週期疲勞問題 (N >= 104 ),S-N 曲線能以簡化後的形式表達:
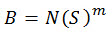 (方程式 7)
(方程式 7)
其中 B 及 m 是材質屬性,包含不同的負載及環境條件,並由疲勞測試實驗決定。
因隨機負載疲勞產生的累積損害 E[AD] 是以 Palmgren-Miner 的規則為根據,且表示為:
 (方程式 8)
(方程式 8)
其中 n(S) 為套用在應力範圍層級 S 的週期數,p(S) 是應力範圍的可能性密度函數。 於上述方程式中代入簡化的 S-N 曲線的數學關係式,隨機應力回應的疲勞損壞一般數學關係式可從以下取得:
 (方程式 9),其中 T 是隨機負載的持續時間 (秒)。
(方程式 9),其中 T 是隨機負載的持續時間 (秒)。
根據方程式 9,有三種方法可用於估計疲勞損害: Steinberg 的三頻方法、窄頻方法及 Wirshing 方法。 每種方法都對於可能性密度函數 p(S) 使用了不同的定義。
窄頻方法
在窄頻方法中,窄頻訊號峰值的可能性密度函數會朝向 Rayleigh 分佈(Bendat J.S., Probability Functions for Random Responses. NASA report on Contact NASA-5-4590, 1964)。
 (方程式 10)
(方程式 10)
於 (方程式 9) 中代入 (方程式 10),並將結果整合至下列疲勞損害估計值的表達式中。
 (方程式 11),其中 Γ(.) 為伽馬函數。
(方程式 11),其中 Γ(.) 為伽馬函數。
Wirsching 方法
Wirsching 方法 (Wirshing, P.H., Paez, T.L., and Ortiz K., Random Vibration, John Wiley & Sons Inc., New York, 1995) 使用經驗修正係數修改「窄頻方法」,將寬頻程序列入考量。
 (方程式 12)
(方程式 12)
 ,(方程式 13)
,(方程式 13)
ζw 是從蒙地卡羅模擬導出的經驗係數,當中包括各種頻譜密度函數。
αw 和 bw 為最適合的參數,計算公式如下:
 (方程式 14)
(方程式 14)
Steinberg 三頻方法
Steinberg 方法假定隨機應力回應的可能性密度函數會遵循高斯分佈,因此應力回應振幅預期的值會受到某些可能性層級所限:
- 應力週期的振幅有 68.27% 的可能性將不會超過 2 乘上應力回應訊號均方根的範圍。
- 應力週期的振幅有 27.1% 的可能性將不會超過 4 乘上應力回應訊號均方根的範圍。
- 應力週期的振幅有 4.3% 的可能性將不會超過 6 乘上應力回應訊號均方根的範圍。
沒有任何應力週期發生大於 6 乘上均方根的範圍。
預期的疲勞損害計算公式如下:
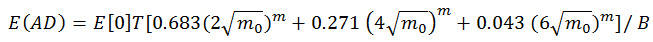 (方程式 15)
(方程式 15)
在模擬中,應力 PSD 函數是來自疲勞研究所根據的動態 - 隨機振動研究的結果。 計算因為所有這三種方法造成的預期損害時會考慮到 vonMises 應力零組件。