Ogden gerinim enerjisi yoğunluğu fonksiyonu şu şekilde tanımlanır:

burada: λi ana uzatma değerleridir; αi, μi malzeme sabitleridir; N, fonksiyondaki terim sayısıdır ve kauçuk benzeri malzemelerin büyük deformasyon aralığının açıklamasında en başarılı fonksiyonlardan biri olarak görülür.
Ogden modelinin formülasyonunda kullanılan ceza işlevi, Mooney-Rivlin modelinde kullanılanın şeklini almıştır. Gerçekte kullanılan gerinim enerjisi fonksiyonu, Ogden fonksiyonunun değiştirilmiş bir türüdür:
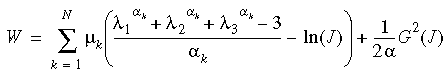
Burada J, deforme hacmin deforme olmamış hacme oranıdır; N, fonksiyondaki terim sayısıdır G(J) = J2-1, ve
 burada ν, Poisson oranıdır.
burada ν, Poisson oranıdır.
Üç terimli (değiştirilmiş Ogden) modeller yaygın bir şekilde kullanılmaktadır. Programda en fazla dört terimli modeller (N=4) kullanılabilir.
Yukarıda bahsedilen malzeme sabitlerinin yanı sıra Poisson oranı da gereklidir. Çoğu durumda, 0,49 ile 0,499 arasında bir Poisson oranı atanarak tatmin edici sonuçlar elde edilebilir. Ayrıca, önemli ölçüde volümetrik gerinim olmadığı sürece Poisson oranının arttırılması sayısal sonuçlar üzerinde ciddi bir etki meydana getirmeyecektir.
Poisson oranı 0,5'e son derece yakın olduğunda, sertlik matrisindeki negatif diyagonal ifadeler ya da yakınsama yokluğu nedeniyle çözümün sonlandırılmasına neden olabilir.
Ogden modelinin malzeme özellikleri
Malzeme iletişim kutusu yoluyla girilir. Zorunlu miktarlar şunlardır:
- Birinci ila Dördüncü Kuvvet malzeme katsayıları (αi)
- Birinci ila Dördüncü malzeme sabitleri (μi) (sabitlerin sayısına bağlı olarak).
- Poisson oranı