Doğrusal olmayan bir malzeme modelinin tipik gerilim-gerinim eğrisi şu şekildedir:
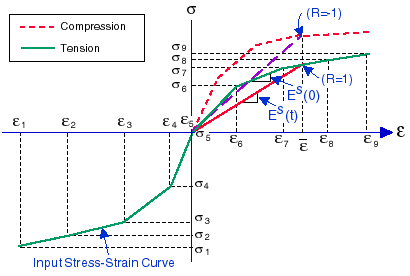
Gerilim tensörü bileşenlerinin monotonik olarak birbirine sabit oranda değiştiği orantılı yükleme içeren bir gerilim geçmişi örneğinde, gerinimler gerilimin nihai durumu açısından aşağıdaki şekilde ifade edilebilir:
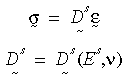
Ds sekant malzeme matrisidir; Es sekant modülüdür ve ν, Poisson oranıdır
Bu modeli uygulamak için Poisson oranı ve bir malzeme gerilim-gerinim eğrisi tanımlanmalıdır.
Kullanıcı tanımlı malzeme (gerilim-gerinim) eğrisinden sekant modülünü elde etmek üzere etkili gerinimi ε(bar) hesaplamak için toplam gerinim vektörü ε kullanılır. Üç boyutlu örnekte:
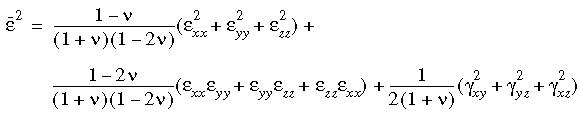
Üçüncü (sıkıştırma) çeyrekten birinci (çekme) çeyreğe kadar gerilim-gerinim eğrisi, bazı değişiklikler yapılarak iki veya üç boyutlu elemanlar için bu modele uygulanabilir. Sekant ve teğet malzeme modüllerini elde etmek için bir interpolasyon yöntemi kullanılır. Volümetrik gerinimin Φ, etkili gerinimin ve Poisson oranının bir fonksiyonu olan R oranı tanımlanırken R şu şekilde ifade edilir:
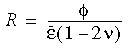
R = 1'in tek eksenli çekme örneğini temsil ettiği ve R = -1'in sıkıştırma örneğini temsil ettiği unutulmamalıdır. Bu iki örnek üst ve alt sınır olarak ayarlanır; böylece, R bu iki değeri aştığında program bunu tekrar limitler dahiline getirir. Doğrusal olmayan elastik malzeme modeli, katı ve kabuk meshleriyle birlikte kullanılabilir.